Spectral-based ConvGNN基础

无向图的拉普拉斯矩阵

拉普拉斯算子

拉普拉斯算子定义为空间标量函数梯度的散度，设有多元函数$f(x_1,…,x_n)$，则其拉普拉斯算子定义为

$\nabla^2 f=\sum_{i=1}^n\frac{\partial^2 f}{\partial x_i^2}$

我们知道标量场在某点的梯度是一个向量，指向该点处变化率最大的方向，模为对应的最大变化率

而向量场在某点的散度是一个标量，描述该点是“正源”还是“负源”，或者说散度是通量的体密度

因此简单来说，拉普拉斯算子描述了标量函数 $f$ 在每一点处的“源”特性

例如对空间温度函数$T(x,y,z)$，拉普拉斯算子$\nabla^2 T$就描述了空间每一点倾向于吸热还是散热

离散函数的拉普拉斯算子

离散函数的导数可以通过泰勒展开来近似

$f(x+\Delta x)=f(x)+f'(x)\Delta x+\frac{1}{2!}f''(x)\Delta x^2+\cdots$

令$\Delta x=\pm 1$可分别得

$f(x+1)=f(x)+f'(x)+\frac{1}{2!}f''(x)+\cdots\\ f(x-1)=f(x)-f'(x)+\frac{1}{2!}f''(x)+\cdots$

于是有离散函数导数的前向差分和逆向差分近似

$f'(x)\approx f(x+1)-f(x)\\ f'(x)\approx f(x)-f(x-1)$

前向和逆向差分相加取平均可得中心差分近似

$f'(x)=\frac{f(x+1)-f(x-1)}{2}$

进一步的，若将$\Delta x=\pm 1$的泰勒展开相加，可得基于中心差分的二阶导数近似

$f''(x)=f(x+1)-2f(x)+f(x-1)$

将该结果拓展到二元离散函数$f(x,y)$得

$\frac{\partial f(x,y)}{\partial x^2}=f(x+1,y)-2f(x,y)+f(x-1,y)\\ \frac{\partial f(x,y)}{\partial y^2}=f(x,y+1)-2f(x,y)+f(x,y-1)$

于是二元离散函数的拉普拉斯算子可表示为

$\begin{aligned} \nabla^2 f(x,y) &=\frac{\partial f(x,y)}{\partial x^2}+\frac{\partial f(x,y)}{\partial y^2}\\ &=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)\\ &=\sum_{(p,q)\in N(i,j)}f(p,q)-f(i,j) \end{aligned}$

其中$N(i,j)$表示与$(i,j)$相邻的点

图像处理中离散拉普拉斯算子常用于边缘检测，用卷积核可表示为

$\begin{bmatrix} 0 & 1 & 0\\ 1 & -4 & 1\\ 0 & 1 & 0 \end{bmatrix}$

拉普拉斯矩阵

记无向图$G=(V,E)$的邻接矩阵为$A$，加权度数矩阵为$D$

其中加权度数矩阵$D=Diag(d1,d_2,…,d_n)$为对角阵，$d_i=\sum_j a{ij}$

设函数$f$为关于图$G$顶点的函数，用列向量$f=(f_1,…,f_n)^T$表示

用类似上节的方法将离散拉普拉斯算子推广到图上，令$\Delta x=\frac{1}{d}$，即边权的倒数，可得

$\nabla^2 f_i=\sum_{j\in N(i)}a_{ij}(f_i-f_j)$

注意此处相对于原始的拉普拉斯算子$f_i,f_j$是对调的，相当于多了一个负号（并没有查到关于这么做的原因）

注意到若$i,j$不是邻居，则$d_{ij}=0$，因此上式可写为

$\nabla^2 f_i=\sum_{j\in V}a_{ij}(f_i-f_j)=\sum_{j\in V}a_{ij}f_i-\sum_{j\in V}a_{ij}f_j=d_if_i-A_if$

将所有顶点的拉普拉斯算子组成列向量得

$\nabla^2 f= \begin{bmatrix} \nabla^2 f_1\\ \vdots\\ \nabla^2 f_n \end{bmatrix} = \begin{bmatrix} d_1f_1-A_1f\\ \vdots\\ d_nf_n-A_nf \end{bmatrix} =\begin{bmatrix} d_1 & & &\\ & d_2 & & \\ && \ddots&\\ && & d_n \end{bmatrix} \begin{bmatrix} f_1\\ f_2\\ \vdots\\ f_n \end{bmatrix} - \begin{bmatrix} A_1\\ A_2\\ \vdots\\ A_n \end{bmatrix} \begin{bmatrix} f_1\\ f_2\\ \vdots\\ f_n \end{bmatrix} =(D-A)f$

其中$L=D-A$就是图的拉普拉斯矩阵

实践中较常用的是拉普拉斯矩阵的归一化形式$L=I_n-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$

拉普拉斯矩阵有一系列重要性质

对称半正定
$n$个特征值满足$0=\lambda_1\leq \lambda_2\leq \cdots\leq \lambda_n$
对应于$\lambda=0$的特征向量一定为$X=(1,1,\cdots,1)^T$
对任意向量$X\in R^n$，有$X^TLX=\frac{1}{2}\sum{i=1}^n\sum{j=1}^na_{ij}(x_i-x_j)^2$

由于拉普拉斯矩阵是实对称阵，因此存在正交阵$U=[u_1,u_2,…,u_n]$和对角阵$\Lambda=diag(\lambda_1,\lambda_2,…,\lambda_n)$使得

$L=U\Lambda U^T$

其中$u_i$是对应于特征值$\lambda_i$的特征向量

傅里叶变换基础

傅里叶级数

傅里叶级数的目标是将周期函数表示为不同频率的正弦函数的和的形式

具体来说，傅里叶级数是将周期函数$f(x)$表示为基${1,\sin x,\cos x,\sin 2x,\cos 2x,\cdots}$的线性组合

由周期为$2\pi$的函数$f(x)$在$[-\pi,\pi]$上诱导出的傅里叶级数为

$f(x)\sim \frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)$

其中系数$a_0,a_n,b_n$满足

$\begin{cases} a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\mathrm{d}x\\ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx\mathrm{d}x\\ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nx\mathrm{d}x \end{cases}$

这里用$\sim$而不是$=$是因为傅里叶级数不一定处处收敛，收敛性可以根据狄利克雷条件判断

对于一般的周期为$T$的函数，我们可以令$t=\frac{2\pi}{T}x$，则$f(x)=f(\frac{2\pi}{T}t)=g(t)$，将$g(t)$按周期为$2\pi$的傅里叶级数展开，再带入$x$，得$f(x)$的傅里叶级数为

$f(x)\sim \frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos \frac{2\pi nx}{T}+b_n\sin \frac{2\pi nx}{T})$

其中

$\begin{cases} a_0=\frac{2}{T}\int_{0}^{T}f(x)\mathrm{d}x\\ a_n=\frac{2}{T}\int_{0}^{T}f(x)\cos \frac{2\pi nx}{T}\mathrm{d}x\\ b_n=\frac{2}{T}\int_{0}^{T}f(x)\sin \frac{2\pi nx}{T}\mathrm{d}x \end{cases}$

利用欧拉公式$e^{ix}=\cos x +i\sin x$可将$\sin,\cos$写成

$\sin x=\frac{e^{ix}-e^{-ix}}{2i},\quad\cos x=\frac{e^{ix}+e^{-ix}}{2}$

于是有复数形式的傅里叶级数

$f(x)=\sum_{-\infty}^{\infty}c_n\cdot e^{i\omega_0 nx}$

其中

$\begin{cases} \omega_0=\frac{2\pi}{T}\\ c_0=\frac{a_0}{2}=\frac{1}{T}\int_{0}^{T}f(x)\mathrm{d}x\\ c_n=\frac{1}{T}\int_{0}^{T}f(x)e^{-i\omega_0 nx} \mathrm{d}x \end{cases}$

傅里叶变换

非周期函数无法直接使用傅里叶级数进行展开，解决思路是用某个$T\to \infty$的周期函数$f_{T}(x)$来近似$f(x)$

令$\omega=n\omega_0$，则有

$f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}f(x)e^{-i\omega x}\mathrm{d}x\right]e^{i\omega x}\mathrm{d}\omega=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega x}\mathrm{d}\omega$

记$\mathcal{F}$和$\mathcal{F}^{-1}$分别为傅里叶变换和逆傅里叶变换，则

$F(\omega)=\mathcal{F}[f(x)]=\int_{-\infty}^{\infty}f(x)e^{-i\omega x}\mathrm{d}x\\ f(x)=\mathcal{F}^{-1}[F(\omega)]=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega x}\mathrm{d}\omega$

对于离散信号$x_n$，其离散傅里叶变换(DFT)和逆离散傅里叶变换(IDFT)为

$X_k=\sum_{n=0}^{N-1}x_n e^{-i\frac{2\pi}{N}kn}\\ x_n=\sum_{n=0}^{N-1}X_k e^{i\frac{2\pi}{N}kn}$

可以说傅里叶变换就是傅里叶级数在非周期函数上的扩展

时域-频域转换

傅里叶级数和傅里叶变换的意义非常深刻且广泛，很难完全阐明，因此这里只是一个通俗的理解

前面说傅里叶级数/变换是将函数表示成不同频率的正弦函数的和的形式，这个过程其实是将函数从时域转换到频域

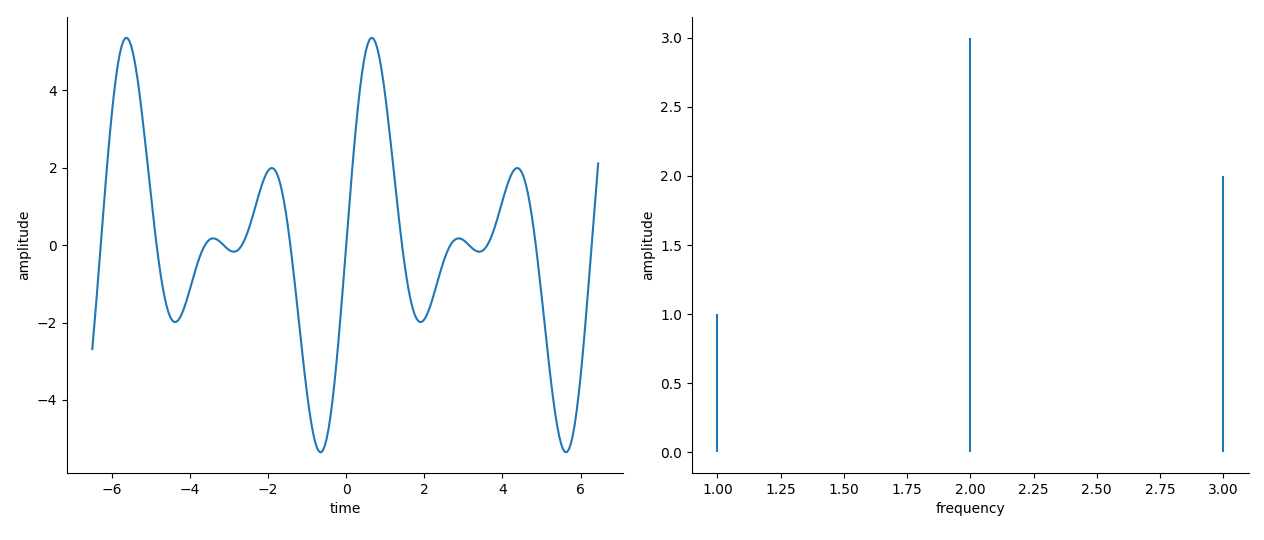
举个例子，对于函数$f(x)=\sin x+3\sin 2x+2\sin 3x$，下图左侧是它的时域图像，横/纵轴分别为时间/振幅；右侧是频域图像，横/纵轴分别为频率/振幅

频域图表明了函数由哪些频率的正弦波组成，不同频率的正弦波所占“比例”各是多少

对于周期函数，傅里叶级数中的系数$c_n$就是不同频率的振幅，因此其频域图是离散的；对于非周期函数，频率$\omega$的振幅就是傅里叶变换$F(\omega)$，因此其频域图是连续的

freq-time

通过将时域-频域转换，我们可以完成很多在时域中难以完成的任务

例如对于一段音频，目标是突出其中的低音，显然直接操作时域波形很难做到，此时我们可以利用傅里叶变换得到其频域谱线，并将高频的振幅减小即可

图傅里叶变换

图的傅里叶变换并不是由傅里叶变换直接推导来的，而是以类比的方式直接定义的

由$\nabla^2 e^{-i\omega x}=-\omega^2 e^{-i\omega x}$知$e^{-i\omega x}$是拉普拉斯算子的本征函数（eigenfunction，不是概率论的特征函数）

而傅里叶变换就是将函数映射到基函数$e^{-iwx}$构成的空间

拉普拉斯算子的本征函数类比到拉普拉斯矩阵中就是特征向量

因此图傅里叶变换就是将图信号映射到拉普拉斯矩阵的特征基${u_1,…u_n}$构成的空间中，即

$\mathcal{F}(\mathbf{x})=\mathbf{U}^T\mathbf{x}\\ \mathcal{F}^{-1}(\mathbf{\hat{x}})=\mathbf{U}\mathbf{\hat{x}}$

其中$\mathbf{x}\in R^n$为无向图的图信号，$x_i$表示第$i$个节点的值

频域图卷积

傅里叶变换的卷积定理指出，函数$f$和$g$的卷积的傅里叶变换等于它们傅里叶变换的乘积，即

$\mathcal{F}(f*g)=\mathcal{F}(f)\cdot\mathcal{F}(g)$

结合图傅里叶变换的定义，可得图信号$\mathbf{x}$关于卷积核$\mathbf{g}\in R^n$的图卷积定义

$\mathbf{x}*\mathbf{g}=\mathbf{U}(\mathbf{U}^T\mathbf{x}\odot\mathbf{U}^T\mathbf{g})$

其中$\odot$表示对应元素相乘

若令$\mathbf{g}_{\theta}=diag(\mathbf{U}^T\mathbf{g})$，则图卷积可表示为

$\mathbf{x}*\mathbf{g}_{\theta}=\mathbf{U}\mathbf{g}_{\theta}\mathbf{U}^T\mathbf{x}$

这就是频域图卷积 (Spectral-based ConvGNN) 的基本形式，不同的图卷积的区别就是$\mathbf{g}_{\theta}$的选择

最初的Spectral-based ConvGNN由Spectral Networks and Deep Locally Connected Networks on Graphs提出，该论文中图卷积层定义为

$\mathbf{H}_{:,j}^{(k)}=\sigma(\sum_{i=1}^{f_{k-1}}\mathbf{U}\mathbf{\Theta}_{i,j}^{(k)}\mathbf{U}^T\mathbf{H}_{:,i}^{(k-1)})\quad(j=1,2,\cdots,f_k)$

其中$\mathbf{g}{\theta}=\mathbf{\Theta}{i,j}^{(k)}$为可学习的对角阵，$\mathbf{H}^{(k-1)}\in \mathbf{R}^{n\times f{k-1}}$为第$k$层的输入图信号，$f{k-1}$为输入通道数，$\mathbf{H}^{(0)}=\mathbf{X}\in \mathbf{R}^{n\times f0}$为原始的多通道图信号，$\sigma$为激活函数，$\mathbf{H}{:,i}$表示第$i$个通道的图信号

容易看出该式种前/后向传播的矩阵乘及拉普拉斯矩阵的特征值分解分别需要$O(n^2)$和$O(n^3)$的复杂度

这种复杂度在实际应用中难以接受，因此该式定义的Spectral GCN并没有广泛应用

后续提出的ChebNet和GCN通过近似的方法显著降低了复杂度，得到了广泛使用

值得注意的是，Spectral-based ConvGNN有一个共同缺点——只能用于Transductive Learning（直推式学习）

Transductive Learning指的是训练时已经有测试数据，预测时只能处理训练时用到的样本

与其相对的是Inductive Learning（归纳学习），模型在预测时需要泛化到未见过的样本，这是一般情况下最常见的学习方式

Spectral-based ConvGNN的卷积使用了归一化拉普拉斯矩阵，而不同的图的拉普拉斯矩阵是不同的，因此训练和推理只能在同一张图上进行