强化学习(3)- TD learning

TD Learning是Value-based RL最常用的算法

Value-based RL的目标是学习最优Q函数$Q^*(s,a)$

然后选择使得Q值最大的动作$a_t=\arg\max_a Q^*(s_t,a)$作为最优策略

我们首先介绍TD Learning的思想，然后介绍几个重要的TD方法——SARSA、Q-learning和DQN

Temporal Difference Learning

时序差分学习(TD Learning)指的是一类算法，其通过自举(bootstrapping)的方式学习value function

我们首先通过一个例子来说明其思想，假设我们需要估计开车从A地到B地的时间$V(A)$，初始估计值$V(A)=10 h$

MC方法的思路是直接完成一次从A地到B地的路程，得到实际的总路程时间$8h$

实际时间与估计值误差为$2h$，于是更新估计值$V(A)\leftarrow 10-2\alpha$，其中常数$\alpha$可视为学习率

而TD Learning的思路是，先从A地开到位于A、B中间的C地，获得其实际路程时间$2h$

设C地到B地的预测时间为$V(C)=7h$，那么$2+7=9h$一定不会是更差的预测

该预测与原估计值误差为$1h$，于是更新更新估计值$V(A)\leftarrow 10-1\cdot\alpha$

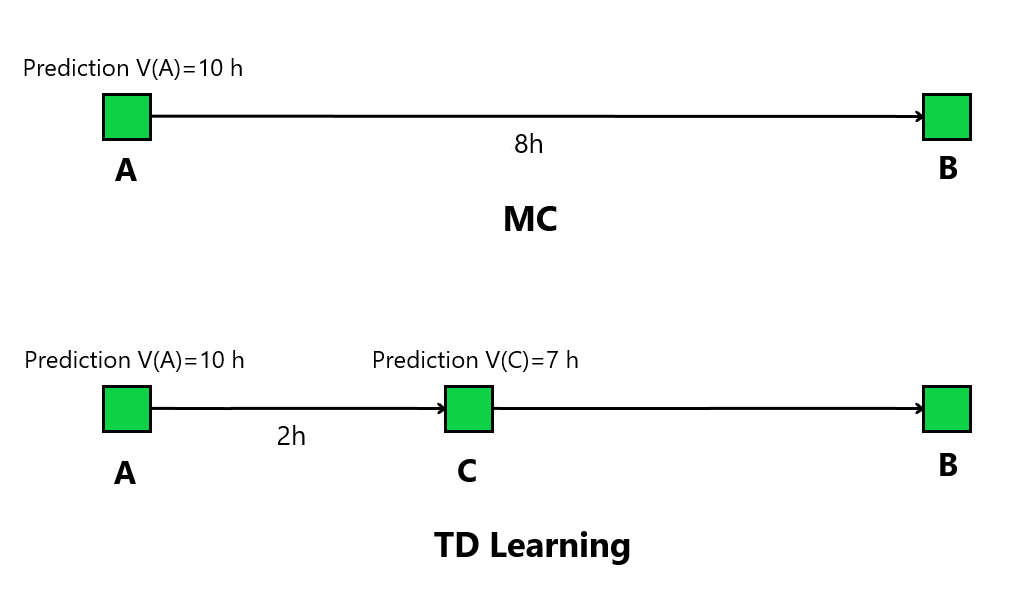
TD Learning of State-Value

通过上面的例子我们可以总结出MC方法估计state-value的公式

$$V(s_t)\leftarrow V(s_t)-\alpha(U_t-V(s_t))$$

以及TD Learning估计state-value的公式

$$V(s_t)\leftarrow V(s_t)-\alpha[V(s_t)-(r_{t+1}+\gamma V_t(s_{t+1}))]$$

该方法称为TD(0)或一步TD，公式中$\delta=r{t+1}+\gamma V_t(s{t+1})$称为TD target，$V(st)-(r{t+1}+\gamma Vt(s{t+1}))$称为TD error

MC和TD Learning最明显的区别就是回合更新和单步更新

一方面，回合更新导致MC的估计方差比TD Learning更大，因为其涉及了更多的随机变量

另一方面，回合更新也使得MC只适用于Episodic task，而TD Learning也适用于Continuing task

SARSA

SARSA使用TD learning的思想来估计action-value

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha\left[r_{t+1}+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t)\right]$$

该公式使用五元组$(st,a_t,r{t+1},s{t+1},a{t+1})$进行更新，因此算法称为SARSA

如伪码所示，公式中$at$是实际发生的动作，即行为策略；$a{t+1}$是仅用于action-value估计的动作，即目标策略，显然两者遵循相同的策略$\pi$，因此SARSA是on-policy方法

SARSA和上一节提到的$\varepsilon$-greedy MC非常相似，其本质不同在于SARSA每次采样一个state-action对后可以立即更新action-value

Q-learning

Q-learning和SARA唯一的不同是TD target取了一个max，也即令Q值直接向$q^*$靠近

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha\left[r_{t+1}+\gamma\max_aQ(s_{t+1},a)-Q(s_t,a_t)\right]$$

一个直观的理解是，既然我们的目标是迭代到$q^*$，与其每次估计当前真实值，不如直接向上限靠近

公式中行为策略$at$遵循策略$\pi$，而目标策略$a{t+1}=\arg\maxa Q(s{t+1},a)$则相当于遵循进行策略提升后的$\pi$，因此Q-learning是off-policy方法

DQN

Deep Q-network (DQN) 是将深度神经网络与Q-learning结合的算法

DQN使用一个神经网络来近似Q函数，其输入为状态$s$，输出$y\in R^{|A|}$为所有动作的Q值$Q(s,\cdot)$，目标是最小化如下目标函数

$$J=E\left[\left(R+\gamma\max_{a\in\mathcal{A}(S^{\prime})}\hat{q}(S^{\prime},a,w)-\hat{q}(S,A,w)\right)^2\right]$$

DQN的训练使用了两个关键的技术，第一个是经验回放(experience replay)

经验回放是指将收集到的样本$(s,a,r,s’)$存入回放缓存(replay buffer) $B={(s,a,r,s’)}$，并按照均匀分布从$B$中采样得到每轮迭代的mini-batch

一般我们假设model的state-action对$(s,a)$服从均匀分布，

而按照某一行为策略产生的样本序列中，相邻样本具有很强的相关性

此时若顺序使用样本，则目标函数的估计偏差将会很大，而经验回放则解决了这一问题

DQN的令一个关键技术是使用两个神经网络

注意到网络参数$w$同时出现在预测值$\hat{q}(S,A,w)$中和TD target $y=R+\gamma\max_{a\in\mathcal{A}(S^{\prime})}\hat{q}(S^{\prime},a,w)$中，导致监督数据目标值不固定，从而难以计算梯度

为此DQN使用了两个网络：Main Network $\hat{q}(s,a,w)$和Target Network $\hat{q}(s,a,w_T)$

在每轮迭代中，对于样本$(s,a,r,s’)$，DQN使用target network计算$yT=R+\gamma\max{a\in\mathcal{A}(s’)}\hat{q}(s’,a,w_T)$，使用main network计算Q的估计值 $y=\hat{q}(s,a,w)$，并使用误差$L=(y-y_T)^2$对main network进行参数更新

每$C$轮迭代之后，将target network参数置为与main network相同，即$w_T=w$