强化学习(2)- DP and MC

动态规划(DP)和蒙特卡洛(MC)都是RL的早期方法，虽然早已不再使用，但它们仍是后续一系列方法的重要基础

DP和MC都属于表格方法(tabular method)，因为其假设MDP的状态空间和动作空间均离散且非常小，从而value function的取值可以用一个表格表示

与之相对的，近似方法(approximation method)用于解决状态/动作空间连续或非常大的情况，其使用一个参数化函数$f(s,a,\theta)$来近似value function

DP

DP方法是一类model-based方法，即MDP的状态转移概率已知

这里介绍两个DP方法——策略迭代 (Policy Iteration) 和值迭代 (Value Iteration)

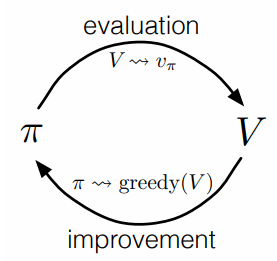
策略迭代方法迭代地进行如下两步以使策略收敛至最优

• 策略评估 (Policy Evaluation) ：对于当前策略$\pi$，计算所有状态对应的state-value $V_{\pi}(s)$
• 策略提升 (Policy Improvement) ：利用策略评估得到的$V_{\pi}(s)$为每个状态寻找更优的策略

值迭代方法直接迭代得到最优的state-value，并通过最优state-value直接得到最优策略

Policy Iteration

对于给定的策略$\pi$，Policy Evaluation旨在计算所有状态的state-value

首先随机初始化$v_0$，然后使用bellman equation进行迭代

$$\begin{aligned} v_{k+1}(s)&=E_{\pi}[R_{t+1}+\gamma v_k(s_{t+1})| s_{t}=s] \\ &=\sum_a\pi(a|s)\sum_{s^{\prime},r}p(s^{\prime},r|s,a)\Big[r+\gamma v_k(s^{\prime})\Big] \end{aligned}$$

该算法称为迭代策略评估 (Iterative Policy Evaluation)

可以证明当迭代次数趋于无穷时，迭代序列${vk}$是收敛于$v{\pi}$的，实际中只要差值足够小时就可以判断为已近似收敛

通过Policy Evaluation我们已经知道当前策略下每个状态的state-value

现在我们想知道能否改变策略获得更好的state-value，即Policy Improvement

假如我们在状态$s$选择一个动作$a\neq \pi(s)$，而后续仍继续服从策略$\pi$，那么新的累积收益为

$$\begin{aligned} q_{\pi}(s,a)&=E[R_{t+1}+\gamma v_{\pi}(s_{t+1})|s_t=s,a_t=a]\\ &=\sum_{s',r}p(s',r|s,a)[r+\gamma v_{\pi}(s')] \end{aligned}$$

若$q(s,a)\geq v_{\pi}(s)$，则说明当前选择动作$a$更好

于是我们可以很自然地得出结论——之后每次在状态$s$选动作$a$都会更好

因此我们可以使用贪心思想为每个状态得到新的策略

$$\pi'(s)=\arg\max_a q_{\pi}(s,a)$$

DP的Policy Iteration就是迭代地进行上述Policy Evaluation和Policy Improvement以获得最优策略的过程

当策略不再变化时，就可以认为已经得到了最优策略

我们一般把遵循这种迭代过程的方法称为广义策略迭代(Generalised Policy Iteration, GPI)

Value Iteration

利用贝尔曼最优方程$v^(s)=\maxa q{\pi^}(s,a)$，我们可以直接迭代得到最优的state-value

$$\begin{aligned} v_{k+1}(s)&=\max_a E[R_{t+1}+\gamma v_k(s_{t+1})\mid s_t=s,a_t=a]\\ &=\max_a\sum_{s^{\prime},r}p(s^{\prime},r|s,a)\Big[r+\gamma v_k(s^{\prime})\Big] \end{aligned}$$

得到近似的$v^*(s)$之后，使用贪心方法就可以得到最优策略

$$\pi^*(s)=\arg\max_a \sum_{s',r}p(s',r|s,a)[r+\gamma v^*(s')]$$

Monte Carlo

MC方法是一种model-free方法，即MDP的状态转移概率未知

MC方法遵循广义策略迭代，不同的是，其policy evaluation对action-value进行估计，因为model-free问题中我们无法根据state-value得到最优策略

而对于policy improvement，MC方法同样采用贪心更新策略

$$\pi(s)=\arg\max_a q(s,a)$$

State-Value估计

尽管MC方法估计的是action-value，但我们仍先以state-value为例来说明MC方法的思想

state-value function定义为$V_{\pi}(s)=E[U_t|s]$，即从状态$s$开始的未来累计折扣收益

对于给定的策略$\pi$，我们可以采样得到多个完整的episode

对于状态$s$，若$s$出现在某个episode中，则可以根据定义利用该episode计算$V{\pi}(s)$，对多个epsiode计算得到的$V{\pi}(s)$取平均即可得到其state-value估计值

显然一个状态$s$可能在同一个episode中出现多次，于是取平均分为两种方法

• 首次访问MC (first-visit MC) ：对同一个episode，只有$s$第一次出现时的$V_{\pi}(s)$参与取平均
• 每次访问MC (every-visit MC) ：对同一个episode，$s$每次出现时的$V_{\pi}(s)$都参与取平均

first-visit MC的伪码如下

基于Exploring Starts的q(s,a)估计

使用MC对action-value进行估计存在一个问题——若使用确定性策略，则对于每个状态$s$只有动作$a=\pi(s)$会被访问，从而不属于策略$\pi$的$q(s,a)$不会被计算，也就无法进行policy improvement

一个简单的方法是每个episode采样开始时随机选择初始$(s,a)$对，称为exploring starts

这种方法下，当episode数趋于去穷时，所有$(s,a)$对的出现数量也都会趋于无穷

$\varepsilon$-greedy MC

显然，实际中Exploring Starts的“无穷”假设很难满足，因此我们介绍另外一种方法

先初始化软策略(soft policy)，即对于任意$s\in S,a\in A$均有$\pi(a|s)>0$

之后在迭代过程中使得$\pi(a|s)$逐渐逼近为确定性策略$\pi(s)$

我们可以使用$\varepsilon$-贪心来实现这个思路——每轮使用当前采样的episode计算得到新的$q(s,a)$后，对于最优动作$a^=\arg\max_a q(s,a)$，更新策略$\pi(a^|s)=1-\varepsilon-\frac{\varepsilon}{|A(s)|}$，对于其他动作，更新策略$\pi(a|s)=\frac{\varepsilon}{|A(s)|}$

我们对该方法下策略的收敛性作一个简单证明，设策略提升后的策略为$\pi’$

$$\begin{aligned} q_{\pi}\left(s,\pi^{\prime}(s)\right) &=\sum_a\pi^{\prime}(a|s)q_\pi(s,a)\\ &=\frac\varepsilon{|A(s)|}\sum_aq_\pi(s,a)+(1-\varepsilon)\max_aq_\pi(s,a)(5.2) \\ &=\geq\frac\varepsilon{|A(s)|}\sum_aq_\pi(s,a)+(1-\varepsilon)\sum_a\frac{\pi(a|s)-\frac\varepsilon{|A(s)|}}{1-\varepsilon}q_\pi(s,a) \\ &=\frac\varepsilon{|A(s)|}\sum_aq_\pi(s,a)-\frac\varepsilon{|A(s)|}\sum_aq_\pi(s,a)+\sum_a\pi(a|s)q_\pi(s,a) \\ &=v_{\pi}(s) \end{aligned}$$

因此策略提升后一定有$\pi’\geq \pi$