强化学习(1)- 基础

基本概念和术语

强化学习 (Reinforcement Learning, RL) 是一种基于行为主义的机器学习方法，其本质是通过交互进行试错学习

RL使用一个由算法控制的智能体agent与环境environment进行互动，互动过程包含下面这些概念：

• state：状态$s_t$表示timestep $t$ 时的完整环境信息
• observation：观测$o$表示状态$s$对agent可见的部分（大多数文献都将两者视为同一概念，并直接用$s$表示）
• action：动作$a_t$是agent观察到状态$s_t$后采取的行动，所有可能的动作集合称为动作空间
• policy：策略控制agent在状态$s_t$下如何选择动作$a_t$，策略可能是确定性的，即$a_t=\pi(s_t)$；或随机性的，即$a_t\sim \pi(a|s_t)$
• reward：奖励$r{t+1}$是采取动作$a_t$后产生的反馈，可表示为$r{t+1}=R(at,s_t,s{t+1})$，这是RL进行学习的依据
• trajectory：轨迹$\tau=(s_0,a_0,s_1,a_1\cdots)$表示agent与环境交互产生的路径
• episode：可译为回合，表示agent与环境交互的一次完整过程

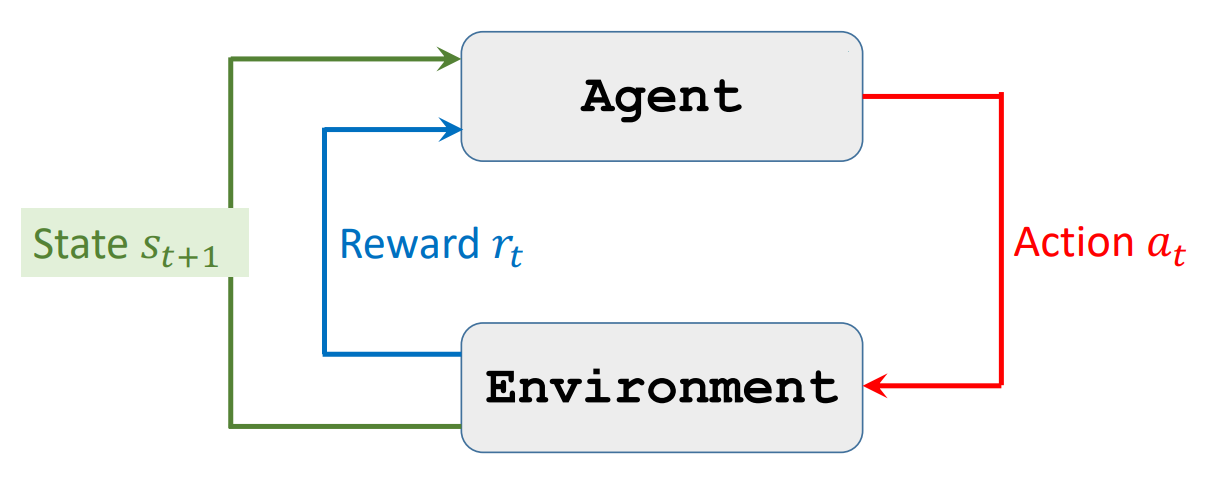
RL的交互就是如下图所示的循环过程：

观察到$s_1$ → 根据$\pi$采取行动$a_1$ → 观察到$s_2$和$r_2$ → 根据$\pi$采取行动$a_2$ → …

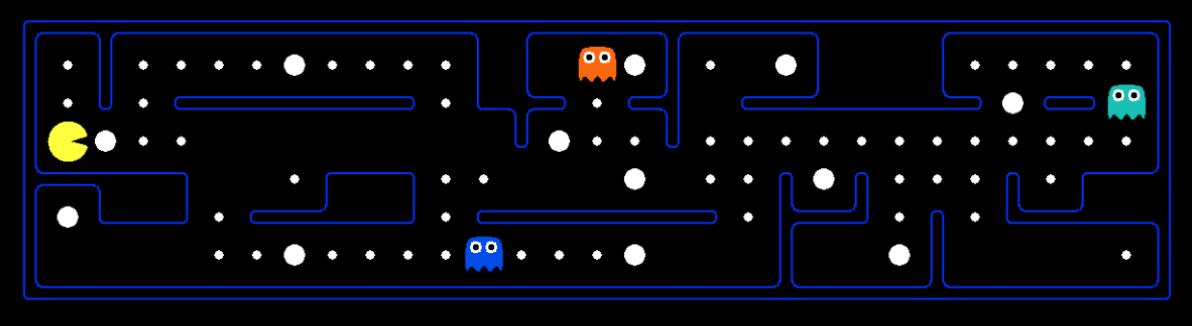
我们可以将这些术语带入pacman进行理解

如图所示，此时图中的一帧就是一个state，其中包含了pacman/ghost/豆子的位置、迷宫信息等等

动作空间为${\uparrow,\downarrow,\leftarrow,\rightarrow}$，reward有几种情况：吃到大豆子$r=100$，吃到小豆子$r=10$，碰到ghost $r=-999999$，其他$r=0$

马尔可夫决策过程MDP

相关基础知识：马尔科夫链基础

RL常常被形式化为马尔可夫决策过程 (Markov Decision Process, MDP) ，即假设状态转移满足马尔可夫性

MDP由四元组$(S,A,P,R)$表示，其中$S$是状态空间，$A$是动作空间，$R(a,s,s’)$是奖励函数，$P$为状态转移转移概率，其满足马尔可夫性，即

$$P(s_{t+1}=s'|s_t=s,a_t=a,s_{t-1},a_{t-1}\cdots,s_0,a_0)=P(s'|s,a)$$

MDP在每个timestep $t$观察到状态$s_t\in S$，并根据某个策略$\pi$选择一个动作$a_t\in A$

之后环境以$P(s{t+1}|s_t,a_t)$的概率转移到下一状态$s{t+1}\in S$，并产生奖励$r{t+1}=R(a_t,s_t,s{t+1})$

这个过程被反复进行下去

若RL的交互总是在进入某些终止状态时停止，则称为回合任务 (episodic tasks)

若RL的交互过程是无限持续的，则称为持续任务 (continuing tasks)

Value Function

强化学习的目标是寻找一个策略$\pi(a|s)$使得累计收益最大化

于是我们引入回报return的概念，其表示某时刻的未来累积折扣收益，记为

$$U_t=r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+1}+\cdots=\sum_{k=0}^{\infty}\gamma^{k} r_{t+k+1}$$

其中$0\leq\gamma\leq1$称为折扣率 (discount rate)

折扣率$\gamma$使得未来越远时刻的收益权重越小，以两个直观的例子理解，即立刻获得100元和将来获得100元显然应选择前者，或者立即获得100元和$T\to \infty$时获得100000000元也应选择前者

为了在互动过程中判断某个状态“有多好”或者选取某个动作“有多好”，我们引入两个价值函数 (value function)

State-Value Function：$V_{\pi}(s_t)=E[U_t|s_t]$

$V_{\pi}(s_t)$表示对于给定的策略$\pi$，从状态$s_t$开始可获得的期望renturn，也即衡量了处于状态$s$有多好

Action-Value Function： $Q_{\pi}(s_t,a_t)=E[U_t|s_t,a_t]$，也即所谓的Q函数

$Q_{\pi}(s_t,a_t)$表示对于给定的策略$\pi$，在状态$s_t$下选择动作$a_t$可获得的期望renturn，也即衡量了在状态$s$下选择动作$a$有多好

Bellman Equation

根据定义我们不难得出两个value function之间的关系

$$\begin{aligned} V_{\pi}(s)&=\sum_{a\in A}\pi(a|s)Q_{\pi}(s,a)\\ Q_{\pi}(s,a)&=\sum_{s'\in S}p(s',r|s,a)[r+\gamma v_{\pi}(s')]\\ \end{aligned}$$

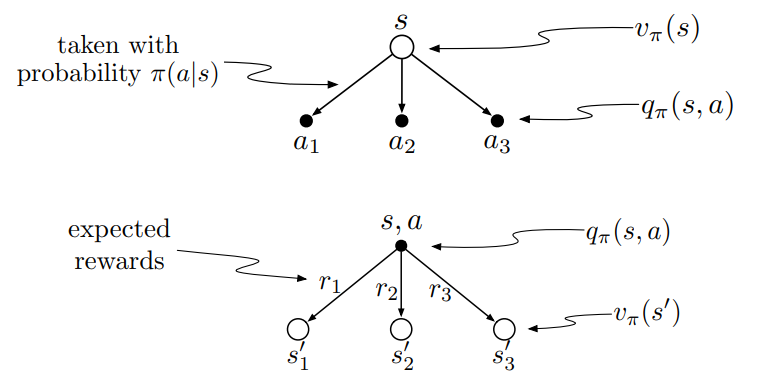
通过两者之间的转换关系，我们可以将value function表示为递归形式

$$\begin{aligned} V_{\pi}(s)=&\sum_{a\in A}\pi(a|s)\sum_{s'\in S}p(s',r|s,a)[r+\gamma v_{\pi}(s')]\\ =&E_{\pi}\left[R_{t+1}+\gamma V_{\pi}(s_{t+1})|s_t=s\right] \end{aligned}$$ $$\begin{aligned} Q_{\pi}(s,a)&=\sum_{s'\in S}p(s',r|s,a)\left[r+\gamma \sum_{a'\in A}\pi(a'|s')Q_{\pi}(s',a')\right]\\ &=E_{\pi}\left[R_{t+1}+\gamma Q_{\pi}(s_{t+1},a_{t+1})|s_t=s,a_t=a\right] \end{aligned}$$

这两个等式称为贝尔曼期望方程 (Bellman Expectation Equation)

最优价值函数

我们将最优value function定义为

$$\begin{aligned} V^*(s)&=\max_{\pi}V_{\pi}(s),\quad \forall s\in S\\ Q^*(s,a)&=\max_{\pi}Q_{\pi}(s,a),\quad \forall s\in S,\forall a\in A \end{aligned}$$

并定义策略$\pi$之间的偏序关系

$$\pi \geq \pi' \quad if \quad V_{\pi}(s)\geq V_{\pi'}(s), \quad \forall s\in S$$

在此基础上，定义最优策略$\pi^$为*使得value function最优的策略

显然在这个定义下最优策略可能有多个，但它们都有相同的最优value function

接下来的问题是如何找到最优策略，考虑下式

$$V_{\pi}(s)=\sum_{a\in A}\pi(a|s)Q_{\pi}(s,a)\leq \sum_{a\in A}\pi(a|s)\left[\max_{a'\in A}Q_{\pi}(s,a')\right]=\max_{a\in A}Q_{\pi}(s,a)$$

由于$\suma \pi(a|s)=1$，为了使等号成立，也即使$V{\pi}(s)$最优，显然最优策略应该直接选择使得$Q$值最大的动作$a$，即

$$\pi^*(a|s)=\begin{cases} 1, & if\ a=\arg\max_a Q(s,a)\\ 0 ,& otherwise \end{cases}$$

于是我们可以得到

$$V^*(s)=\max_{a\in A}Q_{\pi^*}(s,a)$$

该式称为贝尔曼最优方程 (Bellman optimal equation)，通过一些简单推到我们也能得到其递归形式

$$V^*(s_t)=\max_a E_{s_{t+1}}[R_{t+1}+\gamma V^*(s_{t+1})|s_t,a]$$

同理对于Q函数则有

$$Q^*(s,a)=E_{s_{t+1}}[R_{t+1}+\gamma \max_{a'} Q^*(s_{t+1},a')|s,a]$$

对于model-based问题，若$V^*$已知，那么对于当前状态$s$，最优策略就是选择满足贝尔曼最优方程的动作

而对于model-free问题，若$Q^$已知，则最优策略就是选择使得$Q^$最大的动作$a$

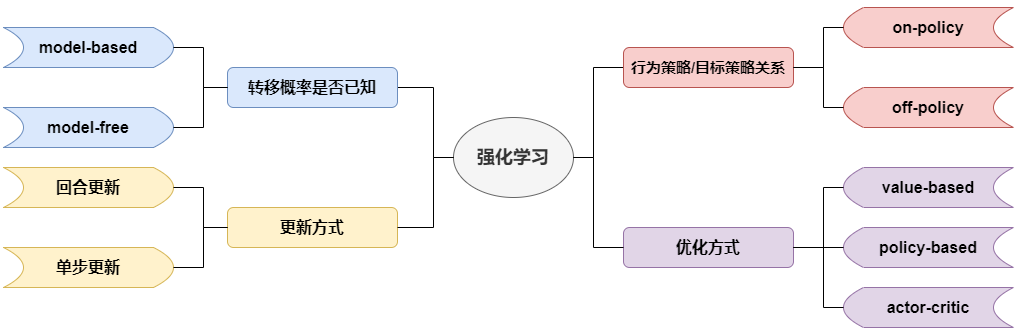
强化学习分类

• 转移概率是否已知

model-based：状态转移概率已知，此时算法可以对下一个state进行预测

model-free：状态转移概率未知，此时agent只能通过观测得知下一个state

两者名字中的model指的是对环境的建模

• 更新方式

回合更新：指RL算法每个episode结束更新一次参数，例如蒙特卡罗方法

单步更新：指RL算法每个timestep更新一次参数，例如Time-Difference Learning (TD Learning)

• 优化方式

value-based：学习得到$Q^(s_t,a_t)$，则为选择使得Q值最大的动作$a_t=\arg\max_a Q^(s_t,a)$

policy-based：直接学习策略$\pi$

action-critic：相当于value-based和policy-based的结合

• 行为策略与目标策略的关系

行为策略 (behavior policy) ：指控制agent与环境交互的策略，行为策略控制实际动作的产生，但不影响Q值的估计

目标策略 (target policy) ：指正在学习的策略，也即作为算法结果的策略，目标策略用于Q值的估计，但不控制实际动作

on-policy：指行为策略和目标策略一致，可译为同策略或在线策略

off-policy：指行为策略和目标策略不一致，可译为异策略或离线策略

举个通俗的例子——off-policy：B用自己的玩法（行为策略）玩pacman，A观察B的操作结果改进自己的玩法（目标策略）；on-policy：A用自己的玩法（行为策略）玩pacman，并根据结果改进自己的玩法（目标策略）