Spatial-based ConvGNN基础

相关论文链接：

GNN综述：A Comprehensive Survey on Graph Neural Networks

NN4G：Neural Network for Graphs: A Contextual Constructive Approach

MPNN：Neural message passing for quantum chemistry

Spatial-based ConvGNN

和spectral-based不同，Spatial-based直接将图像卷积推广到了图上

CNN中卷积操作通过计算$k\times k$小区域中像素值的加权平均作为其中心点的卷积值

类似的，Spatial-based ConvGNN将中心节点及其邻居节点的特征分别处理并进行聚合（称为aggregation，例如求和、平均、加权等）后作为中心节点的卷积值

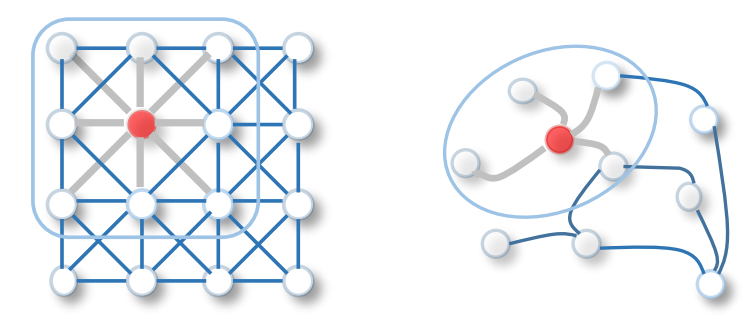
以下做一个统一的符号定义

$\mathbf{x}\in R^n,\mathbf{X}\in R^{n\times d}$分别表示原始的单通道/多通道图节点特征，$\mathbf{x}_v\in R^d$表示节点$v$的原始节点特征，$\mathbf{X}^e\in R^{m\times c}$表示边的特征

$\mathbf{h}_v^{(k)}\in R^{d’}$为第$k$层节点$v$的特征，$\mathbf{H}^{(k)}\in R^{n\times d’}$表示第$k$层节点特征的矩阵形式

$D,A$分别为图的度数矩阵和邻接矩阵，$N(v)$表示节点$v$的邻居节点集合

NN4G

NN4G (Neural Network for Graph) 是首个提出的Spatial-based ConvGNN

NN4G的卷积就是简单的对来自邻居节点的信息求和，即

$$\mathbf{h}_v^{(k)}=f(\mathbf{W}^{(k)^T}\mathbf{x}_v+\sum_{u\in N(v)}\mathbf{\Theta}^{(k)^T}\mathbf{h}_u^{(k-1)})$$

特别的，$h^{(0)}=0$

在此基础上，NN4G还使用了类似residual connection的思想，将前面卷积层的输出都输入当前层，表达式为

$$\mathbf{h}_v^{(k)}=f(\mathbf{W}^{(k)^T}\mathbf{x}_v+\sum_{i=1}^{k-1}\sum_{u\in N(v)}\mathbf{\Theta}^{(k)^T}_{k,i}\mathbf{h}_u^{(i)})$$

将上式表示为矩阵形式得

$$\mathbf{H}^{(k)}=f(\mathbf{X}\mathbf{W}^{(k)}+\sum_{i=1}^{k-1}\mathbf{A}\mathbf{H}^{(i)}\mathbf{\Theta}^{(k)}_{k,i})$$

NN4G的形式其实和GCN非常相似，GCN的卷积形式为$\mathbf{X}*\mathbf{g}_{\Theta}=f\left((\mathbf{I}_n+\mathbf{D}^{-\frac{1}{2}}\mathbf{A}\mathbf{D}^{\frac{1}{2}})\mathbf{X}\mathbf{\Theta}\right)$

两者最重要的差别在于NN4G使用未规范化的邻接矩阵，可能造成$h_v$的尺度无法控制

MPNN

MPNN (Message Passing Neural Networks) 概括了spatial-based ConvGNN的基本框架

$$\mathbf{m}_v^{(k)}=\sum_{u\in N(v)}M_k(\mathbf{h}_v^{(k-1)},\mathbf{h}_u^{(k-1)},\mathbf{x}_{vu}^e)\\ \mathbf{h}_v^{(k)}=U_k(\mathbf{h}_v^{(k-1)},\mathbf{m}_v^{(k)})$$

其中$U_k(\cdot),M_k(\cdot)$是具有可学习参数的方程

对于graph-based任务，MPNN将所有节点特征输入可学习的readout函数$R(\cdot)$以获得图表示

$$\mathbf{h}_G=R(\mathbf{h}_v^{(K)}|v\in V)$$

通过改变$U_k(\cdot),M_k(\cdot),R(\cdot)$，MPNN可以表示很多不同的Spatial-based ConvGNN