DDPM论文浅析

论文链接：Denoising Diffusion Probabilistic Models

这篇论文的贡献主要有两个

1. 证明扩散模型确实有能力生成高质量样本
2. 证明扩散模型的一种特定参数化方法与降噪分数匹配(denoising score matching)等价

一些主要前置知识：

变分推理（Variational Inference）

扩散模型：Deep Unsupervised Learning using Nonequilibrium Thermodynamics

Score Matching：Estimation of Non-Normalized Statistical Models by Score Matching

Score-based Generative Model：Generative Modeling by Estimating Gradients of the Data Distribution

另一篇非常好的参考博客：https://aman.ai/primers/ai/diffusion-models/

Diffusion Model

设$\mathbf{x}{0}$为已知数据集中的样本，它来自分布$q(\mathbf{x}{0})$

设$\mathbf{x}_1,…,\mathbf{x}_T$是与$\mathbf{x}_0$维度相同的隐变量，它们通过一个固定的马尔可夫链采样得到

该马尔可夫链定义为根据方差表$\beta_1,…,\beta_T$逐步向$x_0$中添加随机高斯噪声，称为前向过程(forward process)或扩散过程(diffusion process)

$$q(\mathbf{x}_{t}|\mathbf x_{t-1}):=\mathcal{N}(\mathbf x_t;\sqrt{1-\beta_t}\mathbf x_{t-1},\beta_t\mathbf I)$$

前向过程的一个重要性质是可以解析地在任意timestep进行对$x$采样，令$\alphat=1-\beta_t$，$\overline{\alpha}_t=\prod{s=1}^t\alpha_s$，则有

$$q(\mathbf x_t|\mathbf x_0)=\mathcal N(\mathbf x_t;\sqrt{\bar\alpha_t}\mathbf x_0,(1-\bar\alpha_t)\mathbf I)$$

---

证明：

使用重参数化(reparameterize)技巧，设$\epsilon \sim \mathcal N(\mathbf 0,\mathbf I)$，则

$$\begin{aligned} \mathbf x_t &= \sqrt{\alpha_t}\mathbf x_{t-1} + \sqrt{1-\alpha_t} \mathbf \epsilon_{t-1} \\ &= \sqrt{\alpha_t}\left(\sqrt{\alpha_{t-1}}\mathbf x_{t-2} + \sqrt{1-\alpha_{t-1}} \mathbf \epsilon_{t-2}\right) + \sqrt{1-\alpha_t} \mathbf \epsilon_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf x_{t-2} + \sqrt{\alpha_t-\alpha_t\alpha_{t-1}}\epsilon_{t-2} + \sqrt{1-\alpha_t} \mathbf \epsilon_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}}\mathbf x_{t-2} + \sqrt{(\alpha_t-\alpha_t\alpha_{t-1})+(1-\alpha_t)}\epsilon_{t-2}^*\\ &= \sqrt{\alpha_t \alpha_{t-1}}\mathbf x_{t-2} + \sqrt{1-\alpha_t\alpha_{t-1}}\epsilon_{t-2}^*\\ &= ...\\ &= \sqrt{\bar\alpha_t}\mathbf x_0 + \sqrt{1-\bar\alpha_t}\epsilon_0 \\ \end{aligned}$$

---

采样得到隐变量序列后，可以得到后验$q(\mathbf{x}_{1,T}|\mathbf{x}_0)$

$$q(\mathbf{x}_{1:T}|\mathbf{x}_0):=\prod\limits_{t=1}^{T}q(\mathbf{x}_t|\mathbf{x}_{t-1})$$

现在再定义另一个逆向马尔可夫链，其初始分布为$p_{\theta}(\mathbf{x}_T)=\mathcal{N}\left(\mathbf{x}_T;\mathbf{0},\mathbf{I}\right)$，转移概率是通过学习得到的高斯分布，称为逆过程(reverse process)

$$p_{\theta}\left(\mathbf{x}_{t-1}|\mathbf{x}_{t}\right):=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t}, t\right), \boldsymbol{\Sigma}_{\theta}\left(\mathbf{x}_{t}, t\right)\right)$$

进一步可得联合分布$p{\theta}\left(\mathbf{x}{0: T}\right)$

$$p_{\theta}\left(\mathbf{x}_{0: T}\right):=p\left(\mathbf{x}_{T}\right) \prod_{t=1}^{T} p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$$

扩散模型(Diffusion Models, DM)的思路是用$p{\theta}(\mathbf x{t-1}|\mathbf xt)$来近似$q(\mathbf x{t-1}|\mathbf x{t})$，这样$p{\theta}(\mathbf{x}{0})=\int p{\theta}\left(\mathbf{x}{0: T}\right)d \mathbf{x}{1: T}$就成为了真实分布$q(\mathbf{x}_{0})$的近似

通俗的说，DM对样本不断加噪直到几乎只有高斯噪声，然后再学习加噪的逆过程，即从高斯噪声不断降噪直到获得一个样本

$p{\theta}(\mathbf{x}{0})$的训练是通过优化变分下界进行的，即

$$\mathbb E_q\left[-\log p_{\theta}(\mathbf x_0)\right] \leq\mathbb E_q \left[ -\log\frac{p_{\theta}(\mathbf x_{0:T})}{q(\mathbf x_{1:T}|\mathbf x_0)} \right] =\mathbb E_q \left[ -\log p(\mathbf x_T)-\sum\limits_{t\geq1}\log\dfrac{p_{\theta}(\mathbf x_{t-1}|\mathbf x_t)}{q(\mathbf x_{t}|\mathbf x_{t-1})} \right]=:L$$

直接计算这个式子需要MCMC采样，方差会比较大，因此将$L$进一步改写为

$$L=\mathbb{E}_{q}[\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right) \| p\left(\mathbf{x}_{T}\right)\right)}_{L_{T}}+\sum_{t>1} \underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right) \| p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\right)}_{L_{t-1}} \underbrace{-\log p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}_{L_{0}}]$$

---

证明：

$$\begin{aligned} L=&\mathbb E_q \left[ -\log p(\mathbf x_T)-\sum\limits_{t\geq1}\log\dfrac{p_{\theta}(\mathbf x_{t-1}|\mathbf x_t)}{q(\mathbf x_{t}|\mathbf x_{t-1})} \right]\\ =&\mathbb E_q \left[ -\log p(\mathbf x_T)-\log\dfrac{p_{\theta}(\mathbf x_{0}|\mathbf x_1)}{q(\mathbf x_{1}|\mathbf x_{0})}-\sum\limits_{t>1}\log\dfrac{p_{\theta}(\mathbf x_{t-1}|\mathbf x_t)}{q(\mathbf x_{t}|\mathbf x_{t-1})} \right]\\ =&\mathbb E_q \left[ -\log p(\mathbf x_T)-\log\dfrac{p_{\theta}(\mathbf x_{0}|\mathbf x_1)}{q(\mathbf x_{1}|\mathbf x_{0})}-\sum\limits_{t>1}\log\dfrac{p_{\theta}(\mathbf x_{t-1}|\mathbf x_t)}{q(\mathbf x_{t-1}|\mathbf x_{t}, \mathbf x_{0})}\cdot \dfrac{q(\mathbf x_{t-1}|\mathbf x_{0})}{q(\mathbf x_{t}|\mathbf x_{0})} \right]\\ =&\mathbb E_q \left[ -\log p(\mathbf x_T)-\log\dfrac{p_{\theta}(\mathbf x_{0}|\mathbf x_1)}{q(\mathbf x_{1}|\mathbf x_{0})}-\log \dfrac{q(\mathbf x_{1}|\mathbf x_{0})}{q(\mathbf x_{T}|\mathbf x_{0})}-\sum\limits_{t>1}\log\dfrac{p_{\theta}(\mathbf x_{t-1}|\mathbf x_t)}{q(\mathbf x_{t-1}|\mathbf x_{t}, \mathbf x_{0})} \right]\\ =&\mathbb E_q \left[ -\log \dfrac{p(\mathbf x_T)}{q(\mathbf x_{T}|\mathbf x_{0})}-\log p_{\theta}(\mathbf x_{0}|\mathbf x_1)-\sum\limits_{t>1}\log\dfrac{p_{\theta}(\mathbf x_{t-1}|\mathbf x_t)}{q(\mathbf x_{t-1}|\mathbf x_{t}, \mathbf x_{0})} \right]\\ =&\mathbb E_q \left[ D_{KL}(q(\mathbf x_{T}|\mathbf x_{0})\|p(\mathbf x_T)) +\sum\limits_{t>1}D_{KL}\left(q(\mathbf x_{t-1}|\mathbf x_{t}, \mathbf x_{0})\|p_{\theta}(\mathbf x_{t-1}|\mathbf x_t)\right)-\log p_{\theta}(\mathbf x_{0}|\mathbf x_1) \right] \end{aligned}$$

---

改写后的$L$含义更加明显了，最小化$L$其实就是最小化$D{KL}(q(\mathbf x{t-1}|\mathbf x{t})|p{\theta}(\mathbf x{t-1}|\mathbf x_t))$，也即令$p{\theta}(\mathbf x{t-1}|\mathbf x_t)$和$q(\mathbf x{t-1}|\mathbf x_{t})$尽可能相似

$L{t-1}$中$q(\mathbf{x}{t-1}|\mathbf{x}{t}, \mathbf{x}{0})$根据贝叶斯公式可得

$$q\left(\mathbf{x}_{t-1}| \mathbf{x}_{t}, \mathbf{x}_{0}\right) =\mathcal{N}\left(\mathbf{x}_{t-1} ; \tilde{\boldsymbol{\mu}}_{t}\left(\mathbf{x}_{t}, \mathbf{x}_{0}\right), \tilde{\beta}_{t} \mathbf{I}\right) \\ where \quad \tilde{\boldsymbol{\mu}}_{t}\left(\mathbf{x}_{t}, \mathbf{x}_{0}\right):=\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_{t}}{1-\bar{\alpha}_{t}} \mathbf{x}_{0}+\frac{\sqrt{\alpha_{t}}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_{t}} \mathbf{x}_{t} \quad and \quad \tilde{\beta}_{t}:=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}} \beta_{t}$$

正态分布间的KL散度是可以直接计算的，这样就避免了MCMC

Score-based Model

Score Matching最初的目的是计算非归一化概率模型的归一化常量

其论文中将Score Function定义为对数概率密度的梯度（the gradient of the log-density）

$$\boldsymbol{\psi}(\boldsymbol{\xi} ; \boldsymbol{\theta})=\left(\begin{array}{c}\frac{\partial \log p(\boldsymbol{\xi} ; \boldsymbol{\theta})}{\partial \xi_1} \\ \vdots \\ \frac{\partial \log p(\boldsymbol{\xi} ; \boldsymbol{\theta})}{\partial \xi_n}\end{array}\right) =\nabla_{\boldsymbol{\xi}} \log p(\boldsymbol{\xi} ; \boldsymbol{\theta})$$

Score-based Model的目标是训练是一个分数网络$\mathbf s_{\theta}(\mathbf x)$来估计数据的Score Function，即

$$\frac{1}{2}\mathbb{E}_{p_{\mathrm{data}}}\left[\|\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x})-\nabla_{\mathbf{x}}\log p_{\mathrm{data}}(\mathbf{x})\|_{2}^{2}\right]$$

由于数据的Score Function是未知的，该式需要进一步推导，可以证明，该式在常数差距内等价于

$$\mathbb{E}_{p_{\mathrm{data}}(\mathbf{x})}\bigg[\operatorname{tr}(\nabla_{\mathbf{x}}\mathbf{s}_{\theta}(\mathbf{x}))+\frac{1}{2}\left\|\mathbf{s}_{\theta}(\mathbf{x})\right\|_2^2\bigg]$$

此时$\operatorname{tr}(\nabla{\mathbf{x}}\mathbf{s}{\theta}(\mathbf{x}))$仍是难以计算的，不同的Score-based Model目标就是解决这个问题

一种比较常用的方法是降噪分数匹配（denoising score matching）

其首先使用一个噪声分布$q_{\sigma}(\tilde{\mathbf x}|\mathbf x)$对数据点$\mathbf x$进行搅动，然后使用分数网络估计搅动后的数据分布

$$\frac{1}{2} \mathbb{E}_{q_{\sigma}(\tilde{\mathbf{x}} \mid \mathbf{x}) p_{\text {data }}(\mathbf{x})}\left[\left\|\mathbf{s}_{\boldsymbol{\theta}}(\tilde{\mathbf{x}})-\nabla_{\tilde{\mathbf{x}}} \log q_{\sigma}(\tilde{\mathbf{x}} \mid \mathbf{x})\right\|_{2}^{2}\right]$$

可以证明该式最小化时有$\mathbf{s}^*{\boldsymbol{\theta}}(\tilde{\mathbf{x}})=\nabla{\mathbf{x}} \log q{\sigma}(\mathbf{x})$，当噪声足够小时$q{\sigma}(\mathbf{x})\approx p_{data}(\mathbf x)$

获得了分数网络$\mathbf s{\theta}(\mathbf x)$后，我们可以使用Lagevin Dynamics（或称Lagevin Sampling）从Score Function $\nabla{\mathbf x} p_{\mathrm{data}}(\mathbf{x})$中进行采样，它是一种MCMC采样方法

给定固定步长$\epsilon > 0$、先验分布$\pi$和初始值$\tilde{\mathbf{x}}_0 \sim \pi(\mathbf x)$，Lagevin Sampling循环计算

$$\tilde{\mathbf{x}}_{t}=\tilde{\mathbf{x}}_{t-1}+\frac{\epsilon}{2} \nabla_{\mathbf{x}} \log p\left(\tilde{\mathbf{x}}_{t-1}\right)+\sqrt{\epsilon} \mathbf{z}_{t}$$

其中$\mathbf{z}t\sim \mathcal N(0, I)$，当$\epsilon \to 0, T\to \infty$时，$\tilde{\mathbf{x}}{t}$（在一些正则条件下）就是$p(\mathbf x)$的准确采样

Diffusion Models and Denoising Autoencoders

通过指定不同的$\betat$和不同的逆向过程$p{\theta}\left(\mathbf{x}{t-1}|\mathbf{x}{t}\right)$的参数化形式，可以得到扩散模型的很多不同实现

下面要讨论的一种实现将使扩散模型产生与降噪分数匹配等价的效果

对于$\beta_t$，我们将其固定为常数，此时后验$q$无可学习参数，进而$L_T$也是常数，因此可以忽略

对于逆向过程 $p{\theta}\left(\mathbf{x}{t-1}|\mathbf{x}{t}\right):=\mathcal{N}\left(\mathbf{x}{t-1} ; \boldsymbol{\mu}{\theta}\left(\mathbf{x}{t}, t\right), \boldsymbol{\Sigma}{\theta}\left(\mathbf{x}{t}, t\right)\right)$

首先，令$\boldsymbol{\Sigma}{\theta}\left(\mathbf{x}{t}, t\right)=\sigma_t^2 \mathbf I$，其中$\sigma^2_t$是常量且相互独立，不参与训练

从实验结果来看，$\sigma^2t=\beta_t$和$\sigma^2_t=\tilde{\beta}{t}$具有相似效果（但是论文中的解释暂时没看懂）

The first choice is optimal for $\mathbf x_0 \sim \mathcal N (\mathbf0, \mathbf I)$, and the second is optimal for $x_0$ deterministically set to one point. These are the two extreme choices corresponding to upper and lower bounds on reverse process entropy for data with coordinatewise unit variance.

此时我们可以根据正态分布间的KL散度公式进一步推导得

$$L_{t-1}=\mathbb{E}_{q}\left[\frac{1}{2 \sigma_{t}^{2}}\left\|\tilde{\boldsymbol{\mu}}_{t}\left(\mathbf{x}_{t}, \mathbf{x}_{0}\right)-\boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t}, t\right)\right\|^{2}\right]+C$$

其中$C$是与$\theta$无关的常量

前面提到前向过程可以在任意时间步采样，即$q(\mathbf x_t|\mathbf x_0)=\mathcal N(\mathbf x_t;\sqrt{\bar\alpha_t}\mathbf x_0,(1-\bar\alpha_t)\mathbf I)$

我们对其使用重参数化技巧，令$\epsilon \sim \mathcal N(\mathbf 0,\mathbf I)$，则 $\mathbf xt(\mathbf x_0, \epsilon)=\sqrt{\bar\alpha_t}\mathbf x_0+\sqrt{1-\bar\alpha_t}\epsilon$，将其带入$L{t}$得

$$\begin{aligned} L_{t-1}-C & =\mathbb{E}_{\mathbf{x}_{0}, \boldsymbol{\epsilon}}\left[\frac{1}{2 \sigma_{t}^{2}}\left\|\tilde{\boldsymbol{\mu}}_{t}\left(\mathbf{x}_{t}\left(\mathbf{x}_{0}, \boldsymbol{\epsilon}\right), \frac{1}{\sqrt{\bar{\alpha}_{t}}}\left(\mathbf{x}_{t}\left(\mathbf{x}_{0}, \boldsymbol{\epsilon}\right)-\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}\right)\right)-\boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t}\left(\mathbf{x}_{0}, \boldsymbol{\epsilon}\right), t\right)\right\|^{2}\right] \\ & =\mathbb{E}_{\mathbf{x}_{0}, \boldsymbol{\epsilon}}\left[\frac{1}{2 \sigma_{t}^{2}}\left\|\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}\left(\mathbf{x}_{0}, \boldsymbol{\epsilon}\right)-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \boldsymbol{\epsilon}\right)-\boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t}\left(\mathbf{x}_{0}, \boldsymbol{\epsilon}\right), t\right)\right\|^{2}\right] \end{aligned}$$

从这个推导结果容易得到，对于均值$\mathbf \mu_{\theta}(x_t,t)$，我们应将其参数化为

$$\begin{aligned} \boldsymbol{\mu}_{\theta}(\mathbf{x}_{t},t )=\tilde{\mu}_{t}\left(\mathbf{x}_{t},\frac{1}{\sqrt{\bar{\alpha}_{t}}}(\mathbf{x}_{t}-\sqrt{1-\bar{\alpha}_{t}}\epsilon_{\theta}(\mathbf{x}_{t}))\right)=\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon_{\theta}(\mathbf{x}_{t},t)\right) \end{aligned}$$

其中$\mathbf xt$是给定的模型输入，$\epsilon{\theta}$是根据$\mathbf x_t$预测$\epsilon$的近似函数

确定均值的参数化方法后，$L_{t}$可化简为

$$\mathbb{E}_{\mathbf{x}_0,\epsilon}\left[\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha}_t)}\left\|\epsilon-\epsilon_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\epsilon,t)\right\|^2\right]$$

此时可以明显看出该式与降噪分数匹配非常类似，实际上是在多个尺度的噪声下进行降噪分数匹配，其中的$\epsilon_{\theta}$就相当于学习到的数据梯度

下面给出该参数化方法下扩散模型的算法伪码，如Algorithm2所示，采样$\mathbf x{t-1}\sim p{\theta}(\mathbf x{t-1}|\mathbf x_t)$即计算$\mathbf{x}{t-1}=\frac{1}{\sqrt{\alphat}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon\theta(\mathbf{x}_t,t)\right)+\sigma_t\mathbf{z}$，其中$z \sim \mathcal N(\mathbf 0,\mathbf I)$，这个过程与Langevin dynamics类似

Discrete Decoder of Reverse Process

由RGB表示的图像中每个像素点离散地在${0,1,…,255}$中取值，但现在逆过程中每一步都是连续的高斯分布

为了获得离散似然，我们需要将逆过程的最后一步改写为一个独立的离散解码器(independent discrete decoder)

以下我们假设所有图像的像素值都从$[0,255]$均匀的缩放到了$[-1,1]$

由于上述推导中假定逆过程的协方差矩阵是对角阵，所以显然有

$$p_{\theta}(\mathbf x_0|\mathbf x_1) =\prod_{i=1}^D p_{\theta}(\mathbf x_0^i|\mathbf x_1^i) =\prod_{i=1}^D\mathcal{N}\left(x ; \mu_{\theta}^{i}\left(\mathbf{x}_{1}, 1\right), \sigma_{1}^{2}\right)$$

其中$D$是数据的维度

接下来使用分箱进行离散化，即像素点取值在区间$[x-\frac{1}{255},x+\frac{1}{255}]$时视为取离散值$x$，$x=1,2,…,255$，于是有

$$\begin{aligned} p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right) & =\prod_{i=1}^{D} \int_{\delta_{-}\left(x_{0}^{i}\right)}^{\delta_{+}\left(x_{0}^{i}\right)} \mathcal{N}\left(x ; \mu_{\theta}^{i}\left(\mathbf{x}_{1}, 1\right), \sigma_{1}^{2}\right) d x \\ \delta_{+}(x) & =\left\{\begin{array}{ll} \infty & \text { if } x=1 \\ x+\frac{1}{255} & \text { if } x<1 \end{array} \quad \delta_{-}(x)=\left\{\begin{array}{ll} -\infty & \text { if } x=-1 \\ x-\frac{1}{255} & \text { if } x>-1 \end{array}\right.\right. \end{aligned}$$

Simplified training object

作者在实验中发现，将前面推导的得到的训练目标进一步化简可以得到更好的生成效果

$$L_{\text {simple }}(\theta):=\mathbb{E}_{t, \mathbf{x}_{0}, \boldsymbol{\epsilon}}\left[\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_{\theta}\left(\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}, t\right)\right\|^{2}\right]$$

其中$t\sim U(1,T)$，即均匀分布

Experiment

IS和FID是评价（图像）生成模型的常用量化方法

IS（Inception Score）使用Inception Net输出图像$x$的1000维分类向量$y$，并从两方面量化生成图像的质量

• 清晰度：对单一的生成图像，其类别分布的熵应尽可能小，即对于清晰的图片，其属于某一个类别的概率应趋近于1，其余则趋近于0。因此最小化

  $$E_{x\sim p_g}\left[H(p(y\|x))\right]$$

• 多样性：对成批的生成图像，其类别分布的熵应尽量大，即生成模型生成的图像类别因尽可能丰富，因此最大化

  $$H(E_{x\sim p_g}\left[p(y\|x))\right])$$

将前者取负，两者相加后得IS表达式，IS越大，生成图像质量越高

$$IS=\exp\left(E_{x\sim p_g}\left[D_{KL}(p(y|x)\|p(y))\right]\right)$$

FID（Frechet Inception Distance）使用Inception Net-V3并删除最后的分类层，得到图像的2048维特征向量

FID的思想是直接计算真实图像分布和生成图像分布的距离，但图像分布维度过大不易计算，因此使用Inception输出的2048维特征向量计算Frechet Distance，显然FID越小越好

$$FID=\|\mu_x-\mu_g\|^2+tr\left(\Sigma_x+\Sigma_g-2(\Sigma_x\Sigma_g)^{\frac{1}{2}}\right)$$

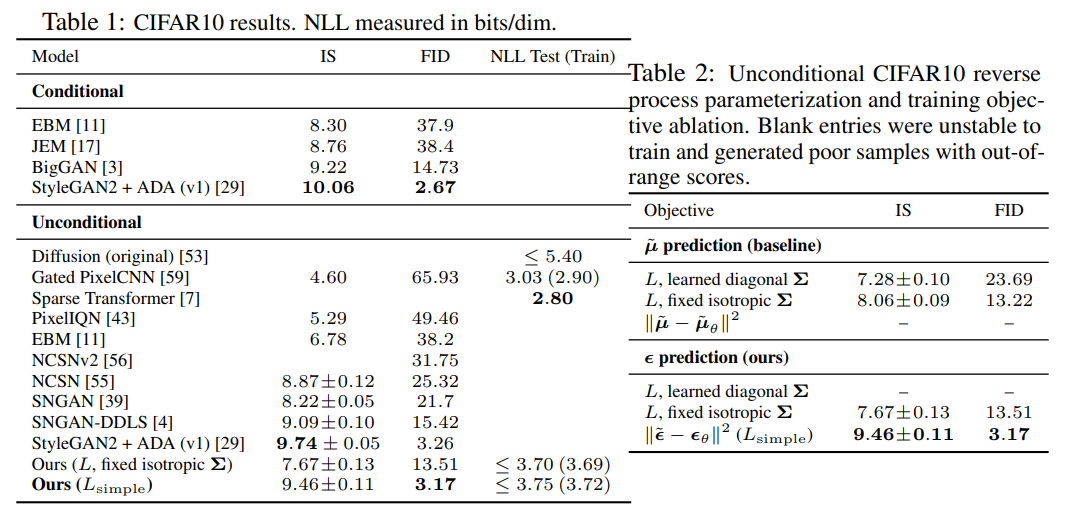
下图Table 1、Table2展示了DDPM的IS、FID和NLL比较

由Tabel 1可知DPPM的IS仅次于StyleGAN2+ADA，而FID则最优，对于负对数似然NLL，论文称使用未化简的变分目标得到的NLL更好，但图片质量不如化简的目标

Table 2对比的是不同的$L$和不同的逆过程参数化方法