VQ-VAE论文解读

论文链接：Neural Discrete Representation Learning

在表示学习(representation learning)中，先前的研究主要关注连续特征

实际上离散表示也与许多模态自然相符，例如语言的离散性就是固有的，语音可以表示为符号序列，图像可以用语言表述

该论文研究了如何将VAE与离散表示结合，称为VQ-VAE (Vector Quantization VAE)

实验中VQ-VAE达到了和连续变量模型相近的压缩效率，并且在图像、音频、视频应用上都展现出了非常好的效果

离散隐变量

首先VAE包含如下几个部分：输入数据$x$，随机隐变量$z$，先验分布$p(z)$，由encoder参数化的后验$q(z|x)$，由decoder建模的$p(x|z)$

VQ-VAE中，我们定义隐嵌入空间为$e\in R^{K\times D}$，其中$K$表示离散隐空间大小，即$K$路标签；$D$是每个隐嵌入向量$e_i$的维度，也即有$K$个嵌入向量 $e_i\in R^D,\ i\in 1,2,…,K$

这里为简便考虑设$z$是一个单独的随机变量，对于图像、音频等应用，$z$可以是2D、3D等

如图所示，输入$x$经过encoder后产生输出$z_e(x)$，再由式(1)计算后验$q(z|x)$

$$q(z=k \mid x)= \begin{cases} 1 & \text { for } \mathrm{k}=\operatorname{argmin}_{j}\left\|z_{e}(x)-e_{j}\right\|_{2} \\ 0 & \text { otherwise } \end{cases} \tag{1}$$

容易看出，该式实际上是一个最近邻查找

通过将$z$定义为均匀分布并结合式(1)，可得KL散度$D_{KL}(q(z|x)|p(z))=1\cdot\log \frac{1}{\frac{1}{K}}=\log K$，从而使得似然$\log p(x)$与ELBO在常数差距上绑定了

接下来用(2)式对$z$进行采样并输入decoder进行重建即可

$$z_q(x)=e_k,\quad \text{where}\quad k=\arg\min_j\|z_e(x)-e_j\|_2 \tag{2}$$

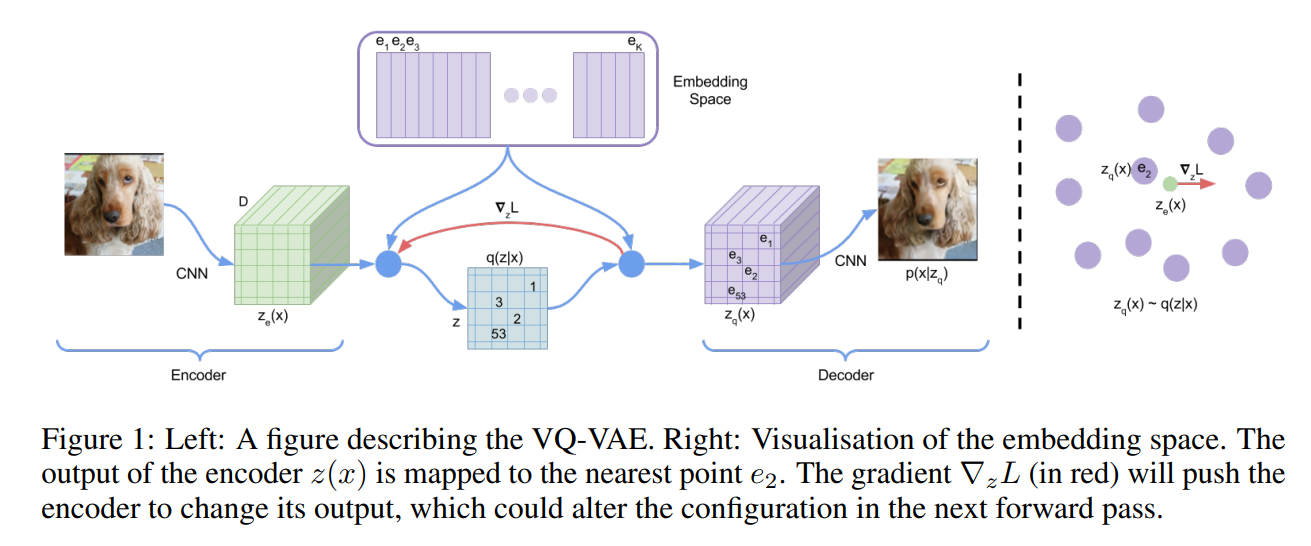
学习过程

注意到式(2)中$\arg\min$是不可导的，也就没有梯度

论文的解决方法是直接将decoder输入$z_q(x)$的梯度复制给encoder输出$z_e(x)$

式(3)是VQ-VAE的完整loss，其中包含3个部分，容易看出第一项是重建损失(reconstruction loss)

由于上述$z_e(x)$到$z_q(x)$的直接梯度复制，嵌入向量$e_i$无法从重建损失中获得梯度

为了学习$e_i$，需要用到Vector Quantisation，即使用$l_2$误差令$e_i$项$z_e(x)$靠近，对应式(3)的第二项，其中$sg$表示stop gradient操作

式(3)第三项称为commitment loss，用于保证encoder输出和嵌入空间保持相近

即由于嵌入空间的体积是无量纲的，如果嵌入向量$e_i$的训练速度没有encoder快，那么嵌入空间就有可能无限制地增长

$$L=\log p\left(x|z_{q}(x)\right)+\left\|\operatorname{sg}\left[z_{e}(x)\right]-e\right\|_{2}^{2}+\beta\left\|z_{e}(x)-\operatorname{sg}[e]\right\|_{2}^{2} \tag{3}$$

综上，decoder由loss第一项训练，encoder由第一、三项训练，嵌入由中间项训练

此外由于KL散度固定为了常数，因此VAE训练中的KL散度项在这里是不需要的

先验选择

如前面所述，VQ-VAE训练时先验$p(z)$是均匀分布

而训练完成后，我们可以用一个自回归(autoregressive)分布拟合$p(z)$，从而可以采用ancestral sampling生成$x$

具体来说，对于图像可以使用PixelCNN，对于音频可以使用WaveNet

图像实验

论文使用VQ-VAE将$x=128\times 128\times 3$的图像压缩到了$z=32\times 32\times 1$的离散空间中，其中$K=512$，decoder是纯反卷积网络

VQ-VAE的压缩率达到了$\frac{128\times 128\times 3\times 8}{32\times 32\times 1\times 9}\approx 42.6$ (bit为单位)，Figure2是其重建效果，重建图像只是有轻微模糊

论文进一步在$32\times 32\times 1$离散隐空间上训练了PixelCNN作为先验

Figure3展示了从PixelCNN中采样并用VQ-VAE的decoder进行重建的效果

论文还设计了一个实验验证VQ-VAE消除了VAE的posterior collapse，即decoder过于强大，可以直接建模$x$，导致隐变量被忽略

作者先在DM-LAB数据集上训练了第一个VQ-VAE，将$84\times84\times3$的帧压缩到$21\times21\times1$，此时在$21\times21\times1$隐空间上重建的图像和原图像几乎没有区别

在此基础上，作者训练了第二个VQ-VAE，将上述$21\times21\times1$隐空间压缩到$3\times 1$隐空间（$21\times21\times1$的样本通过PixelCNN获得），此时隐空间总共只有$3\times 9=27\ bits$，小于float32

用该隐空间重建的图像丢失了许多特征，说明decoder确实是从隐变量中获取信息进行重建的

后面论文还有音频和视频的实验，因为不太了解，所以先挖个坑