论文链接：A Simple Framework for Contrastive Learning of Visual Representations

在对视觉表达(visual representation)的无监督学习问题的研究中，基于对比学习的方法逐渐展现出巨大的潜力

该论文为视觉表达学习引入了一个简单的对比学习框架，即SimCLR(a simple framework for contrastive learning of visual representations)

对比学习框架

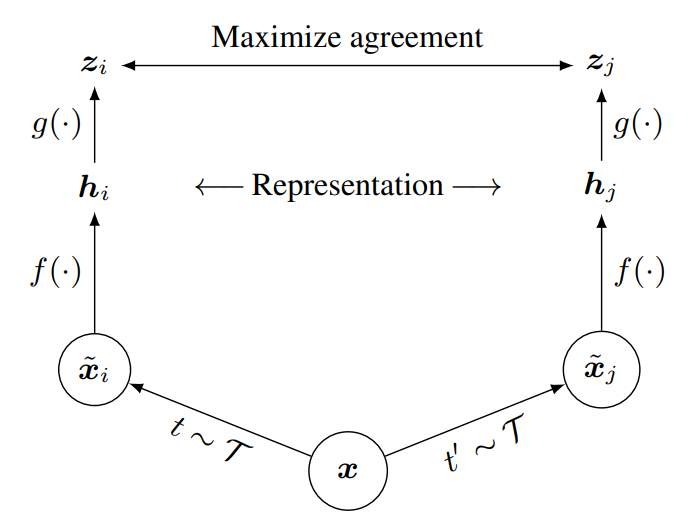
如图所示为SimCLR的基本框架，包括如下几个主要部分

  • 随机数据增强模块：将样本$x$随机转换为$x$的两个相关视图(correlated view)，记为$\widetilde{x_i},\widetilde{x_j}$，表示一个正对(positive pair)，其中增强操作包括随机裁剪、随机颜色失真(color distortion)、随机高斯模糊，这里color distortion包括了color jittering和color drop
  • 编码器$f(\cdot)$：用于从增强后的样本中抽取表示向量(representation vector)，论文采用了ResNet
  • 映射层$g(\cdot)$：将representation向量映射到可应用对比损失的维度，论文使用了仅一个隐层的MLP
  • 对比损失(contrastive loss)函数：用于对比预测任务损失函数，即给定集合${\widetilde{x}_k}$，其中包含正对$(\widetilde{x}_i,\widetilde{x}_j)$，对比预测任务的目标是给定$\widetilde{x}_i$找到对应的$\widetilde{x}_j$

SimCLR

对于大小为$N$的minibatch，通过数据增强将得到$N$个正对，也即$2N$个样本

对于给定的正对$(i,j)$，我们将其他$2(N-1)$个样本都视为负样本(negative samples)

令$\mathrm{sim(u,v)}=u^Tv/|u||v|$，即余弦相似度，则正对$(i,j)$的损失定义为

其中$\mathbb{1}_{[k \neq i]}$表示当且仅当$k\neq i$时为1，而$\tau$则为温度参数

最终损失通过对minibatch中所有正对计算上述损失得到，包括$(i,j)$和$(j,i)$，称为NT-Xent (the normalized temperature-scaled cross entropy loss)

SimCLR_algorithm

模型训练使用ImageNet ILSVRC-2012

模型评估采用的方法是linear evaluation protocol

即冻结base模型，在顶层添加一个线性层进行分类训练，用准确率间接评估representation的质量

数据增强

此前已有的研究都通过改变模型结构来定义出不同的对比预测任务（具体的引用见论文）

例如Hjelm et al. (2018); Bachman et al. (2019)通过限制模型感受野大小，达到了 global-to-local 视图预测的效果

而Oord et al. (2018); Hénaff et al. (2019)通过一个固定的图像分割过程以及一个context aggregation网络，达到了近邻视图预测的效果

如图所示，SimCLR论文提出，简单的随机裁剪就能定义出一个包含上述两者的预测任务

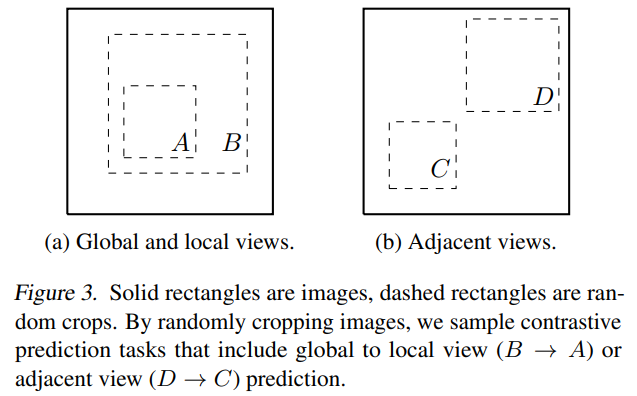
SimCLR_random_cropping

为了定义出更全面和广泛的对比预测任务，论文考虑继续组合其他数据增强方法，如下图所示，研究的增强方式包括

  • 空间/集合变换：裁剪、缩放（同时翻转）、旋转、抠除cutout
  • 外观变换：颜色失真color distortion（包括color dropping、color jittering——亮度、对比度、饱和度、色调）、高斯模糊、Sobel滤波

论文测试了以上单个以及不同组合的数据增强方法对模型的影响

结论是没有任何单个的增强方法足以学习到好的representation

进一步的，其中一个数据增强组合表现最为突出：随机裁剪+随机颜色失真

论文推测这是因为仅应用随机裁剪时，图像的颜色分布仍十分相近

SimCLR_data_augmentation

为了进一步证明数据增强的重要性，论文对不同强度的数据增强做了对比

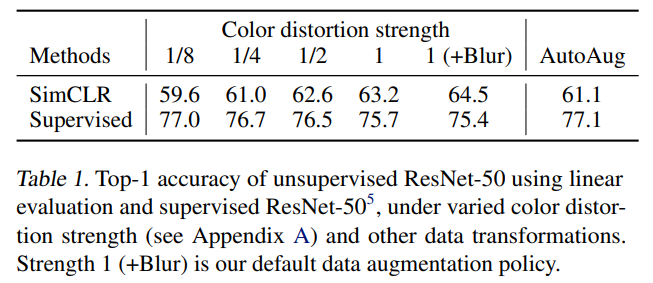
如表所示，更强的数据增强显著提升了linear evaluation的效果，此外Cubuk et al., 2019等人提出的AutoAugment并没有取得比本论文中随机裁剪+强颜色失真更好的效果

另一方面，该表结果还显示出监督方法并没有受益于数据增强

SimCLR_strong_augmentation

模型结构

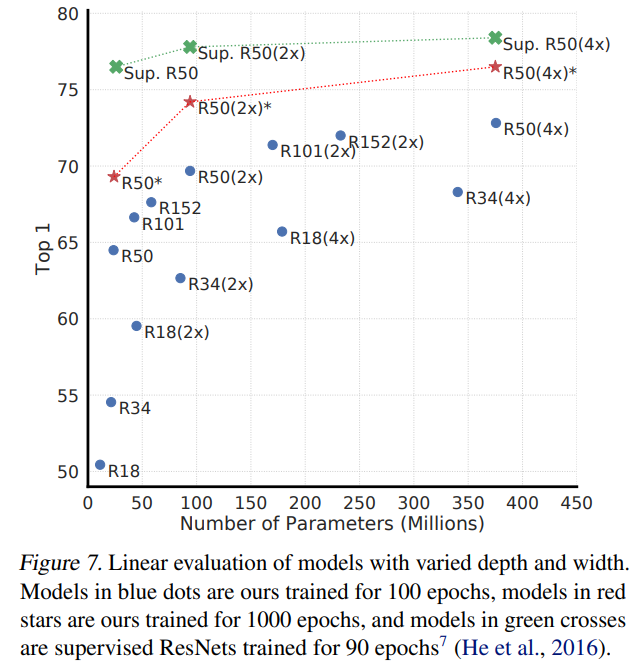
Figure7展示的是对不同encoder大小的实验结果，结论是比较符合直觉的，即增大深度和宽度都能提升效果

从图中还能看出一点，随着模型增大，SimCLR与有监督模型的差距缩小很快，说明与有监督相比，无监督学习从大模型中受益更多

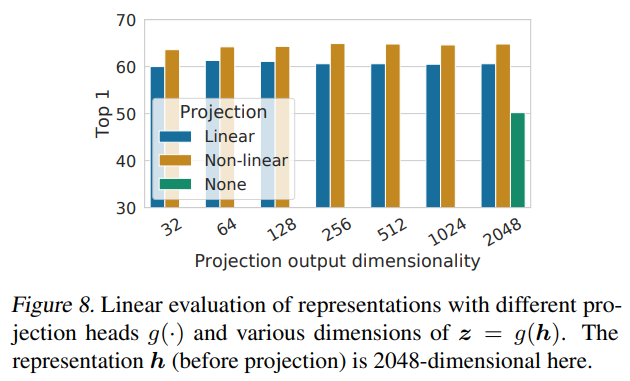
Figure8展示的是对不同映射层$g(\cdot)$的实验结果

由图可知，非线性效果优于线性，远优于无映射层，但映射层不同输出维度对结果影响不大

此外论文称输入映射层前的representation远优于之后的representation，论文推测原因是$z=g(h)$在对比预测任务中被训练成对数据增强具有不变性，从而使得$g$移除了对下游任务有用的信息

为了验证这个猜想，论文构造了一个实验，分别用$h$和$g(h)$预测预训练时使用了什么数据增强，结果确实是$h$的准确率远远高于$g(h)$（更多分析见论文附录）

SimCLR_fig7

SimCLR_fig8

Loss和Batchsize

论文将NT-Xent与一些常用的对比学习损失做了对比，例如Logistic Loss和Margin Loss

理论角度，观察几个loss的梯度，NT-Xent的优点在于l2 normalization和温度参数有效平衡了不同样本，特别是负样本

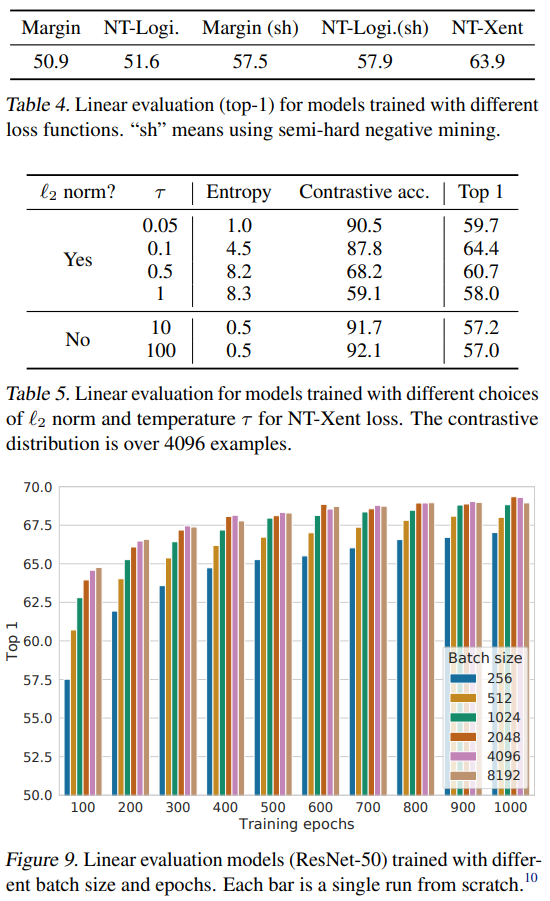
实验角度，论文为几个loss都加了l2 normalization与NT-Xent进行对比，结果如Table 4所示，NT-Xent的优势显然

另一方面，论文也通过控制l2 normalization与温度参数对NT-Xent本身进行了验证

结果如Table 5所示，在有l2 normalization的情况下，温度参数是否合适对效果影响很大，而没有l2 normalization时，虽然对比任务准确率高，但linear evaluation效果降低了

Figure9展示的是batchsize和epoch数对结果的影响

其中epoch较少时，大batchsize对效果提升很大，随着epoch数增加，大batchsize的效果逐渐变得不那么明显

论文称，这是因为对比学习中更大的batchsize和epoch数能提供更多的负样本，促进收敛

SimCLR_loss_batchsize

后面论文与SOTA的比较就不放了，不是很重点