LSGAN详解

论文链接：Least Squares Generative Adversarial Networks

LSGAN的思想

原始GAN采用了Sigmoid+Binary Cross Entropy的损失
其存在一个问题，即G生成的图像G(z)虽然成功地让D认为是真图像，但实际上G(z)仍然和真实的图像x有很大差距
此时由于D已经被欺骗，导致G没有可更新的梯度
最终使得G生成的图像质量仍较低

我们可以根据作者的图来理解

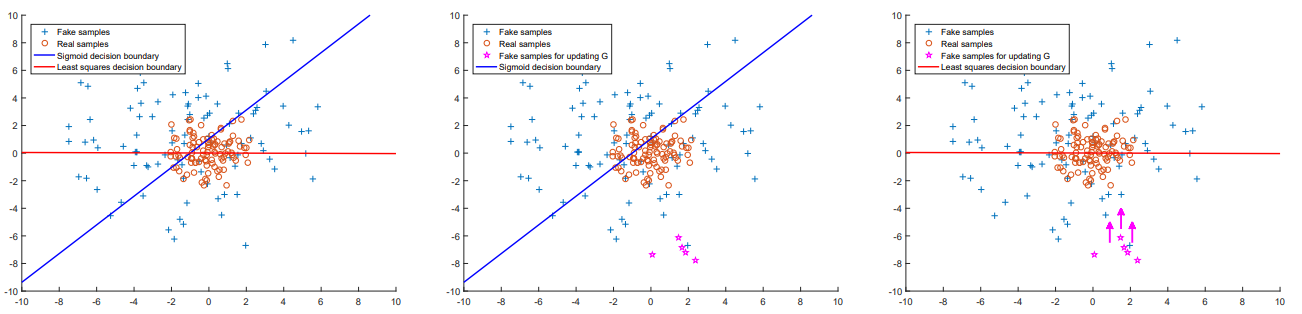
其中蓝点为G生成的假图像，红点为真图像，蓝线和红线分别为原始GAN的D和LSGAN的D的判别界限

当我们试图用被D判别为真的假图像（洋红色点）去更新G的时候
若使用sigmoid+BCE损失，会发现因为loss几乎为0而产生梯度消失

因此作者提出了用least square loss训练GAN
由于成功训练的GAN的D的判别曲线应该是穿过并平分真实图像分布的
而least square loss可以使生成的图像朝判别边界移动，也就同时使得假图像向真图像区域靠拢的目标函数

这种GAN称为LSGAN（Least Square GAN），其数学表达为

$$\underset{D}{min}V_{\mathrm{LSGAN}}(D)=\frac{1}{2}E_{x\sim p_{\mathrm{data}}(x)}[(D(x)-b)^2]+\frac{1}{2}E_{z\sim p_z(z)}[(D(G(z))-a)^2]$$​​​ $$\underset{G}{min}V_{\mathrm{LSGAN}}(G)=\frac{1}{2}E_{z\sim p_z(z)}[(D(G(z))-c)^2]$$​​​ 其中a、b分别为假、真数据的标签，c表示G希望让D判别出的值 ## 损失函数的构造 论文中给出了两种为a、b、c赋值的方法 作者的实验表明**两种方法表现相当** - 令$a=-1,b=1,c=0$​ 可证明该赋值方法可使得当且仅当$p_{\mathrm{d}}(x)=p_g(x)$时G达到最优，具体间下节证明 - 令$b=c$ 根据a、b、c的定义，从直觉上理解即使G生成的图像尽可能真实 可以令$a=0,b=c=1$ ## LSGAN收敛性证明 LSGAN论文和原始GAN论文的证明过程很相似 以下将$p_{\mathrm{data}}$​简记为$p_{\mathrm{d}}$​ ### 最优判别器D 首选对固定的G求最优的D $$\underset{D}{min}V_{\mathrm{LSGAN}}(D) = \frac{1}{2}E_{x\sim p_{\mathrm{d}}(x)}[(D(x)-b)^2]+\frac{1}{2}E_{x\sim p_g(x)}[(D(x)-a)^2] \\ = \frac{1}{2}\int_x p_{\mathrm{d}}(x)(D(x)-b)^2 + p_g(x)(D(x)-a)^2\mathrm{d}x$$​​ 对积分内的式子通过求导求极值，得到​​​最优的D满足 $$D^{*}(x)=\frac{bp_{\mathrm{d}}(x)+ap_g(x)}{p_{\mathrm{d}}(x)+p_g(x)}$$​ ### 最优生成器G 对于固定的已达最优的D，分析最优的G 首先托展$\underset{G}{min}V_{\mathrm{LSGAN}}(G)$​为 $$\underset{G}{min}V_{\mathrm{LSGAN}}(G)=\frac{1}{2}E_{x\sim p_{\mathrm{d}}(x)}[(D(x)-c)^2]+\frac{1}{2}E_{z\sim p_z(z)}[(D(G(z))-c)^2] $$​​​ 然后带入最优的D得到新的训练目标表示 $$2C(G)=E_{x\sim p_{\mathrm{d}}(x)}[(D^{*}(x)-c)^2]+E_{x\sim p_g(x)}[(D^{*}(x)-c)^2] \\ = \int_x (p_{\mathrm{d}}(x)+p_g(x))(\frac{(b-c)p_{\mathrm{d}}(x)+(a-c)p_g(x)}{p_{\mathrm{d}}(x)+p_g(x)})^2 \mathrm{d}x \\ = \int_x \frac{((b-c)(p_{\mathrm{d}}(x)+p_g(x))-(b-a)p_g(x))^2}{p_{\mathrm{d}}(x)+p_g(x)} \mathrm{d}x$$​ 令$b-c=1,b-a=2$ $$2C(G)=\int_x \frac{(2p_g(x)-(p_g(x)+p_{\mathrm{d}}))^2}{p_{\mathrm{d}}(x)+p_g(x)} \mathrm{d}x = \mathcal{X}^2_{\mathrm{Pearson}}(p_{\mathrm{d}}+p_g\| 2p_g)$$

表明当且仅当$p{\mathrm{d}}(x)+p_g(x)=2p_g(x)$​，即$p{\mathrm{d}}(x)=p_g(x)$​时
训练目标C(G)达到最小，也即G可收敛

代码实现

结构上LSGAN和DCGAN完全相同
把损失函数换乘MSE即可