论文链接：Neural Machine Translation By Jointly Learning To Align And Translate

什么是Attention

Seq2Seq解读与实现中讲解的原始的Seq2Seq模型中存在一个问题
即encoder的输出是固定长度的向量
如果输入序列很长，这个定长向量就很可能无法浓缩所有信息

首先很容易想到将encoder每个timestep的输出都保留下来
这样就有了一个尺寸为(timestep, output_dim)的矩阵表示encoder的处理结果（原来seq2seq相当于只保留了这个矩阵最后一行）

那么要如何处理这个矩阵并传递给decoder呢
考虑到人类的翻译过程，我们首先会进行 “我=I” “咖啡=coffee” 这样一个单词对应关系的转化
这个过程称为对齐（alignment）

也就是说人类会专注于一个单词（或短语）进行翻译
我们把这种过程应用于神经网络，就叫Attention机制

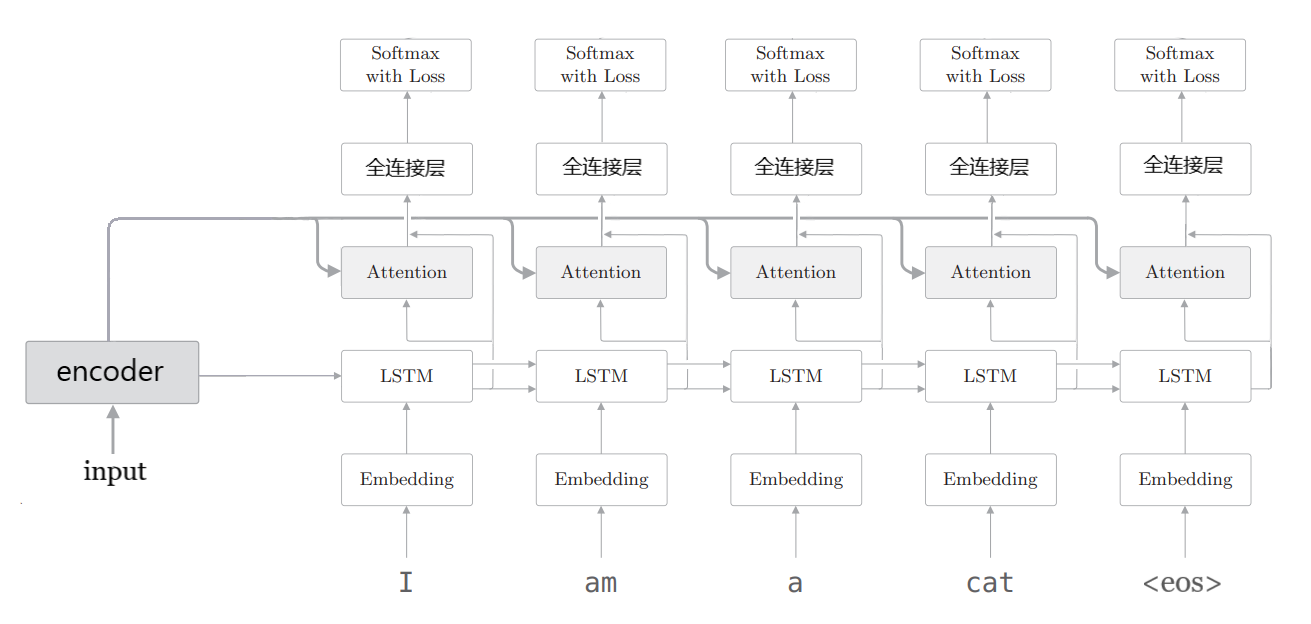
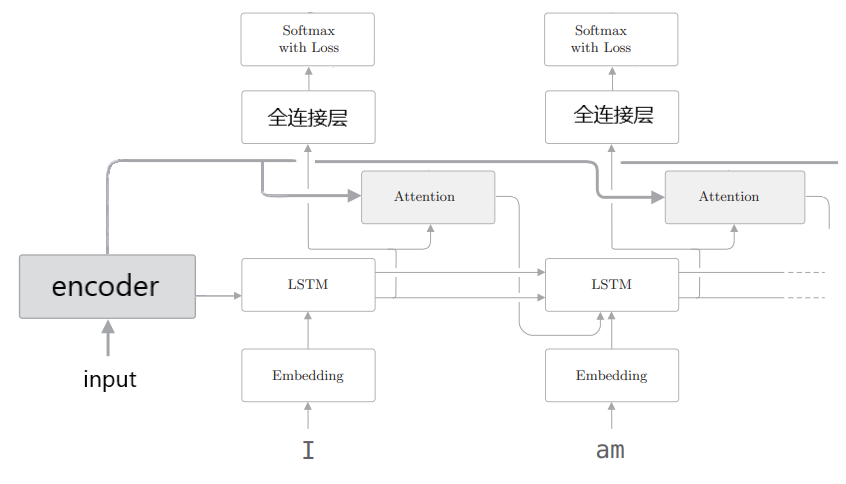
加入Attention机制的seq2seq如图所示
encoder最后一个cell的状态仍然作为decoder的初始状态
不同之处加入了Attention层，用于从encoder所有timestep的输出中选出decoder当前timestep要专注的部分

seq2seq_attention

Attention层的内部原理

记encoder、decoder输出张量分别为$V,Q$​​​​​​​，并设$V,Q$​​​​​ ​尺寸分别为 $(T_V,dim)$​​​​​ ​​和 $(T_Q,dim)$​​​​​​​
其中$T_V,T_Q$​​​​​​​​​分别为encoder、decoder的时间步数量（也即句子最大长度）

理论上$V$​​​​​​​​​（或$Q$​​​​​​​​​​）的第$t$​​​​​​​​行向量主要包含了encoder（或decoder）对输入中第$t$​​​​​​个单词的处理结果
依照前述的对齐思想，对于$Q$​​​​​​的第$i$​​​​​​行，我们想找到它在$V$​​​​​​中最应该专注的一行$j$​​​​​​​​​​​​，并用这两行向量合并处理

然而实际中选择确定的一行并不可行，因为“选择”不是可微分的
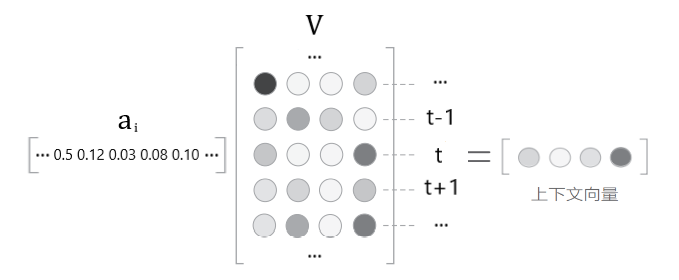
因此对于$Q$​​​​​​的第$i$​​​ ​​行，我们改为给$V$​​​​​​​​​的每一行赋予一个权值，表示对该行的专注度

也即，用一个尺寸为$(1, T_V)$​​权重向量$a_i$​​与$V$​​作矩阵乘法
就得到了一个用加权和表示对 $V$​​ 各行专注度的上下文向量

显然，要计算$Q$每行对$V$的上下文向量，就需要一个尺寸为$(T_Q,T_V)$的权重矩阵​

Attention1

下面再来考虑权重矩阵如何获得

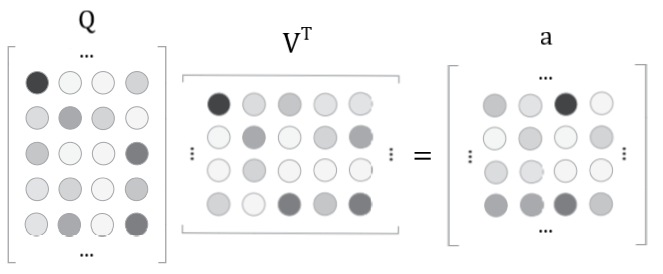
对于$Q$​​的第$i$​​行，权重向量$ai$​​实质上是表示**向量$Q{i,}$​​与$V$​各行向量的相似度**

表示两个向量相似程度的方法有很多，最简单的就是内积
因此，只要矩阵$QV^T$​​就是我们要的权重矩阵$a$​​ ，其第$i$​​行对应$Q_{i,}$​​的权重向量$a_i$​​​
当然还需要对每个行向量$a_i$​​​​进行softmax激活来正规化数值

Attention2

综上整个Attention层的结构如下图所示

Attention3

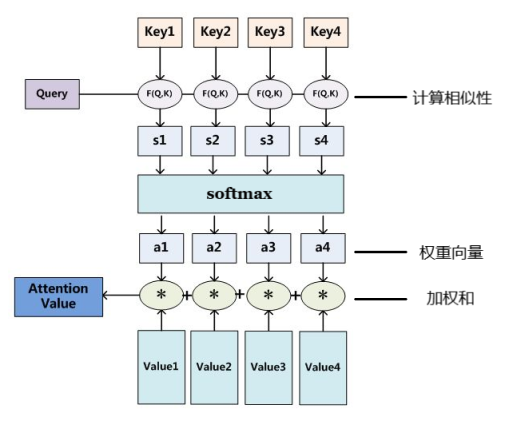
更一般的描述Attention

考虑Attention思想更一般的抽象化描述

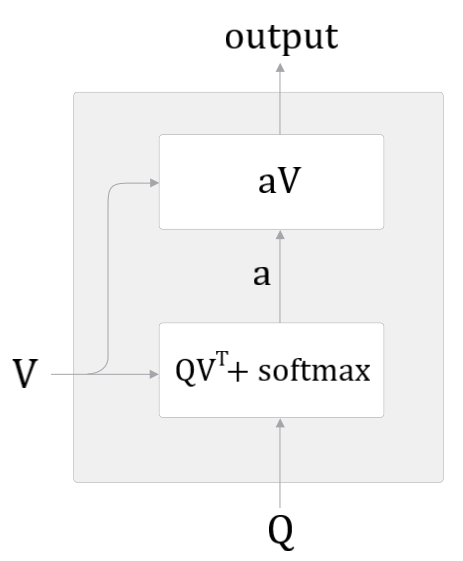
我们已知(Key, Value)张量对以及目标张量Query（分别记为$K,V,Q$​​）
首先计算$Q$​​中特定的一行与$K$​​每一行的相似度，若用点积表示相似度，则相似度矩阵为$QK^T$​​

对$QK^T$​​每一行分别softmax正规化得到权重矩阵$a$​​，表示$Q$​​中特定的一行对$K$​​每一行的专注度
那么Attention的输出就是$aV$​​，表示用加权和描述$Q$​​对$V$​​各行给与不同关注度得到的结果

综上，Attention的数学表达即为

其中输入张量$Q,K,V$​​​​​​​​的尺寸分别为$(samples,T_Q,dim)$​​，$(samples,T_K,dim)$​​，$(samples,T_K,dim)$​​，输出张量尺寸为$(samples, T_Q, dim)$​​​

实际中Key和Value往往是相同的，上述Seq2Seq就是如此

Attention4

Attention的应用方式

前面第一节的图示中是将Attention输出与RNN输出直接进行concatenate再输入全连接层
很多文献中还使用如下图所示的方法利用attention输出

即每个RNN cell的输出计算Attention后，再将Attention结果输入下一个RNN cell
实际中两种方法表现都很优异

seq2seq_attention2

Keras实现带Attention的Seq2Seq

代码中用了English to French sentence pairs数据集，数据预处理见Seq2Seq解读与实现
代码中使用了keras已实现的Attention层，且encoder部分按照论文使用了双向RNN

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
""" Seq2Seq with Attention
    paper: Neural Machine Translation By Jointly Learning To Align And Translate
    see: https://arxiv.org/pdf/1409.0473.pdf
"""

from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, LSTM, Dense, Embedding, Bidirectional, \
    TimeDistributed, Attention, Concatenate
import numpy as np
from keras_tf.NLP.preprocessor import TatoebaPreprocessor  # 数据预处理器


class Seq2Seq:
    def __init__(self):
        preprocessor = TatoebaPreprocessor(dataDir='D:\\wallpaper\\datas\\fra-eng\\fra.txt', num_samples=10000)

        self.text_en, self.text_fra = preprocessor.getOriginalText()
        (self.dict_en, self.dict_en_rev), (self.dict_fra, self.dict_fra_rev) = preprocessor.getVocab()
        num_word_en, num_word_fra = preprocessor.getNumberOfWord()
        self.tensor_input, self.tensor_output = preprocessor.getPaddedSeq()

        self.encoder, self.decoder, self.model = self.buildNet(num_word_en, num_word_fra, 256)

    def buildEncoder(self, num_word, latent_dim):
        inputs = Input(shape=(None,))  # shape: (samples, max_length)
        embedded = Embedding(num_word, 128)(inputs)  # shape: (samples, length, vec_dim)

        outputs, _, _, state_h, state_c = Bidirectional(
            LSTM(latent_dim, return_sequences=True, return_state=True),
            merge_mode='ave'
        )(embedded)

        # only save the last state of (backward RNN of) encoder
        return Model(inputs, [outputs, state_h, state_c])

    def buildDecoder(self, num_word, latent_dim):
        inputs = Input(shape=(None,))   # shape: (samples, max_length)
        embedded = Embedding(num_word, 128)(inputs)  # shape: (samples, length, vec_dim)

        input_state_h = Input(shape=(latent_dim,))
        input_state_c = Input(shape=(latent_dim,))
        lstm = LSTM(latent_dim, return_sequences=True, return_state=True)

        # initial_state(Call arguments): List of initial state tensors to be passed to the first call of the cell
        # Here we use the last state of encoder as the initial state of decoder
        outputs_dec, output_state_h, output_state_c = lstm(
            embedded, initial_state=[input_state_h, input_state_c]
        )

        outputs_enc = Input(shape=(None, latent_dim))
        outputs_atten = Attention()([outputs_dec, outputs_enc])
        x = Concatenate()([outputs_dec, outputs_atten])

        prob = TimeDistributed(Dense(num_word, activation='softmax'))(x)

        return Model(
            [inputs, input_state_h, input_state_c, outputs_enc],
            [prob, output_state_h, output_state_c]
        )

    def buildNet(self, num_word_in, num_word_out, latent_dim):
        encoder = self.buildEncoder(num_word_in, latent_dim)
        decoder = self.buildDecoder(num_word_out, latent_dim)

        inputs_encoder = Input(shape=(None,))
        inputs_decoder = Input(shape=(None,))

        outputs_encoder, state_h, state_c = encoder(inputs_encoder)
        prob, _, _ = decoder([inputs_decoder, state_h, state_c, outputs_encoder])

        model = Model([inputs_encoder, inputs_decoder], prob)

        # there's no need to pass one-hot tensor when using sparse_categorical_crossentropy
        model.compile(optimizer='rmsprop', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

        return encoder, decoder, model

    def trainModel(self, epochs, batch_size):
        # there's one timestep shift when using teach forcing
        outputs_shift = np.zeros(self.tensor_output.shape)
        outputs_shift[:, :-1] = self.tensor_output.copy()[:, 1:]

        self.model.fit(
            [self.tensor_input, self.tensor_output], outputs_shift,
            epochs=epochs, batch_size=batch_size, validation_split=0.2,
        )

        self.test()

    def test(self):
        for idx in range(5):
            input_seq = self.tensor_input[idx: idx + 1]
            translated = self.translate(input_seq)
            print('-')
            print('Input sentence:', self.text_en[idx])
            print('Decoded sentence:', translated)
            print('Ground truth:', self.text_fra[idx])

    def translate(self, input_seq):
        outputs_encoder, state_h, state_c = self.encoder.predict(input_seq)

        # blank target sentence, which only has a <sos> symbol
        cur_word = np.zeros((1, 1))
        cur_word[0, 0] = self.dict_fra['\t']

        max_length = 80
        translated = ''
        for _ in range(max_length):
            outputs, state_h, state_c = self.decoder.predict([cur_word, state_h, state_c, outputs_encoder])

            output_idx = np.argmax(outputs[0, -1, :])
            output_word = self.dict_fra_rev[output_idx]

            # stop when <eos> symbol has been generated
            if output_word == '\n':
                break

            translated += ' ' + output_word

            # next input of decoder
            cur_word = np.zeros((1, 1))
            cur_word[0, 0] = output_idx

        return translated

seq2seq = Seq2Seq()
seq2seq.trainModel(epochs=10, batch_size=64)