马尔可夫随机场MRF和条件随机场CRF

马尔可夫随机场

概率图模型是一类用图来表达变量相关关系的概率模型

使用无向图的模型称为马尔可夫网(Markov Net)或马尔可夫随机场(Markov Random Field, MRF)

假设有联合概率分布$P(X)$，我们可以用无向图$G(V,E)$来表示$P(X)$

$G$中任意一个结点$v\in V$表示一个随机变量$X_v$，而任意边$e\in E$表示其连接的两个结点（随机变量）间的依赖关系

给定概率分布$P(X)$，其对应的无向图模型$G(V,E)$满足：

全局马尔可夫性：假设$G$中结点集合$A$到$B$必须经过节点集合$C$，则给定随机变量子集$X_C$时，随机变量子集$X_A$和$X_B$条件独立，即

$$P(X_A,X_B|X_C)=P(X_A|X_C)P(X_B|X_C)$$

根据全局马尔可夫性，可进一步推论无向图$G$满足：

局部马尔可夫性：设$v\in V$是$G$的任意一个结点，$W$是与$v$邻接的结点的集合，$U=V/({v}\cup W)$是除$v$和$W$外所有结点的集合，则

$$P(X_v,X_U|X_W)=P(X_v|X_W)P(X_U|X_W)$$

也即给定某变量的邻接变量，则其他变量条件独立于该变量

成对马尔可夫性：设$u,v\in V$是$G$的任意两个不直接相连的变量，$W$是除$u,v$外的所有其他变量，则

$$P(X_v,X_u|X_W)=P(X_v|X_W)P(X_u|X_W)$$

无向图模型的因子分解

首先给出团和极大团的定义

团：设$C\subset G$是无向图$G$的结点子集，若$C$中任意两结点间均有边相连，则称$C$为团

极大团：若$C$是无向图$G$的团，且在$C$中加入任意其他结点后$C$不再是团，则称$C$为极大团

将联合概率分布表示为其无向图中极大团上的随机变量的函数的乘积的操作，称为无向图模型的因子分解，即

$$P(X)=\frac{1}{Z}\prod_C \Psi_C(X_C)$$

其中常数$Z$是规范化因子，用于保证$P(X)$的积分为1，其值由下式给出，但实际中$Z$通常是难以计算的

$$Z=\sum_X\prod_C \Psi_C(X_C)$$

函数$\Psi_C(X_C)$称为势函数(potential function)，势函数必须非负，因此常定义为指数形式

$$\Psi_C(X_C)=\exp(-H(X_C))$$

Hammersley-Clifford定理指出：无向图模型的分布一定可以表示为图上所有最大团上的势函数的乘积

条件随机场

条件随机场(Conditional Random Field, CRF)是一种对条件概率进行建模的马尔可夫随机场

具体来说，给定观测序列$X=(X_1,X_2,…,X_N)$和标记序列$Y=(Y_1,Y_2,…,Y_N)$，CRF对$P(Y|X)$进行建模

若随机变量$Y$构成一个由无向图$G=(V,E)$表示的马尔科夫随机场，即

$$P(Y_v|X,Y_{V/\{v\}})=P(Y_v|X,Y_W),\quad where\quad W\sim v$$

则称$G$为概率分布$P(Y|X)$的条件随机场

其中$V/{v}$是除结点$v$外的所有结点，$W$是所有与$v$邻接的结点的集合

虽然图$G$可以有任意结构，但实际中一般关注的是线性链条件随机场(linear chain CRF)，如下图所示

形式化的说，线性链CRF满足$P(Yi|X,Y_1,…,Y{i-1},Y{i+1},…,Y_n)=P(Y_i|X,Y{i-1},Y_{i+1})$

线性链CRF广泛用于NLP等序列处理，例如词性标注任务中，观测序列$X$是单词序列，标记序列$Y$则是词性序列

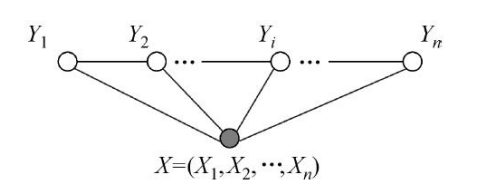
显然线性链CRF上每对相邻的$Y_i$构成一个极大团，每个$Y_i$本身构成一个团，因此$P(Y|X)$可通过因子分解表示为

$$P(Y=y|X=x)=\frac{1}{Z}\exp\left(\sum_k\sum_{i=1}^{n-1} \lambda_kt_k(y_{i-1},y_i,x,i)+\sum_k\sum_{i=1}^{n}\mu_ks_k(y_i,x,i)\right)$$

其中$t_k,s_k$称为特征函数，$t_k$是定义在边上的特征函数，称为转移特征；$s_k$是定义在结点上的特征函数，称为状态特征，特征函数一般取值为1或0，常数$\lambda_k,\mu_k$是相应特征函数的权重

与HMM相同，CRF也关注观测序列概率计算、参数学习和预测三个问题并有相应的算法

（反正传统方法用的不多了所以算法挖个坑以后再填）