变分推断
变分推断
在概率模型中,利用已知变量推断未知变量分布的过程称为推断(或称推理,inference)
假设模型的联合概率分布为$P(X,Z)$,其中$X$是观测变量,$Z$是隐变量和模型参数的集合,推断的目标就是学习模型的后验概率分布$P(Z|X)$,该分布往往很复杂,所以一般使用近似方法
马尔科夫链蒙特卡罗MCMC使用随机抽样的方法来近似该分布
而变分推理(variational inference, VI)则寻找另一个简单的分布$Q(Z)$使其与$P(X|Z)$尽可能相似,称其为变分分布
变分法是泛函分析领域的概念,简单来说泛函是函数的函数,它将函数映射为标量,例如信息熵,而变分法就是寻找泛函的极值
度量两个分布的相似度很容易想到KL散度,将KL散度分解为如下形式
其中$\log P(x)$为证据(evidence),称$L(q)=E_Q[\log P(X,Z)]-E_Q[\log Q(Z)]$为证据下界(evidence lower bound, ELBO)
给定观测数据$X$,则证据可视为常量,因此可通过最大化ELBO来最小化KL散度,此时近似问题就变成了优化问题
从VI角度理解EM算法
关于EM算法的Jensen不等式推导可见 EM算法
EM的目标是寻找参数$\theta$以最大化似然$\ln P(X|\theta)$,而根据上述推导有
因为KL散度大于等于0,所以ELBO就是似然$\ln P(X|\theta)$的下界,也即为最大化似然,只需最大化ELBO
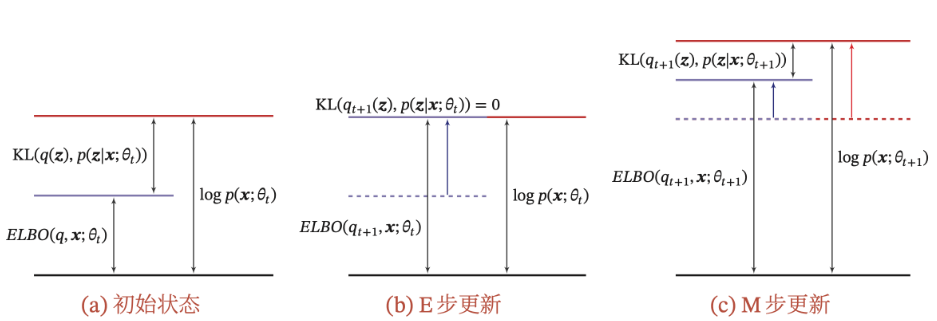
因此有EM算法的E-step:固定参数$\theta$,寻找一个$Q(Z|\theta)$的近似分布使得ELBO最大
显然若$\theta$固定,则$\ln P(X|\theta)$为常数,只需令KL散度等于0,也即假设$Q(Z|\theta)=P(Z|X,\theta)$,ELBO就取到了最大值
获得了$Q(Z|\theta)$的近似分布后则有
也即EM算法的M-step:固定$Q(Z)$,寻找最优参数$\theta$使得ELBO最大
可见VI推导的结果与Jensen不等式推导的结果相同
平均场变分推断
平均场(mean field)是最常用的变分分布的近似假设之一,其假设隐变量间是相互独立的,即
将$Q_k(Z_k)$简记为$q_k$,则
以及
记概率分布$\ln \hat{P}(X,Zj)=E{\prod_{i\neq j}q_i}[\ln P(X,Z)]$,于是有
显然最大化$L(qj)$即最小化$D{KL}(q_j| \hat{P}(X,Z_j))$,因此可以得到分量$Z_j$的最优近似
