蒙特卡罗方法

蒙特卡罗方法简介

蒙特卡罗(Monte Carlo)方法不是某个特定的算法，而是一类随机算法的总称
蒙特卡洛方法依赖于重复随机抽样来获得数值结果，也即使用随机性来解决原则上可能具有确定性的问题

一般来说，随机算法可以分为两类：蒙特卡罗算法和拉斯维加斯算法。

蒙特卡罗算法中采样越多，越近似最优解

例如欲求$N$个数的平均数，可以采用随机抽样取出其中$n<N$个数，以$n$个数的平均值作为近似解
显然$n$越大，近似解越接近正确解，但除非$n=N$，否则永远无法得到正确解

拉斯维加斯算法中采样越多，越可能找到最优解

例如欲找到大数$N$的任意一个因子，可以随机抽取$x<N$并判断$x$是否整除$N$
显然随机的$x$越多就越容易找到$N$的因子，即找到正确解，但也有可能无解

总的来说，蒙特卡罗方法并没有明确的定义，但往往遵循一个特定的模式：

假设概率分布已知，蒙特卡罗通过抽样获得概率分布的随机样本
通过大量随机样本对概率分布的特征进行分析

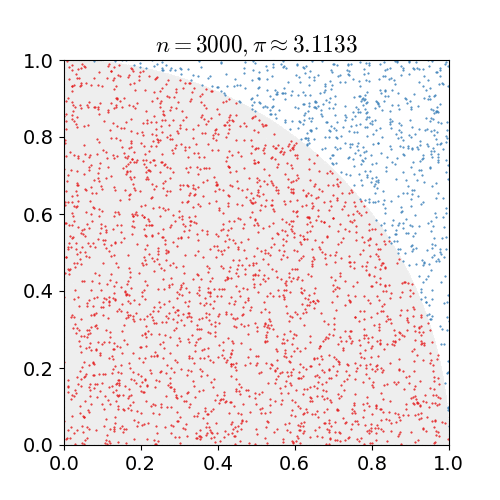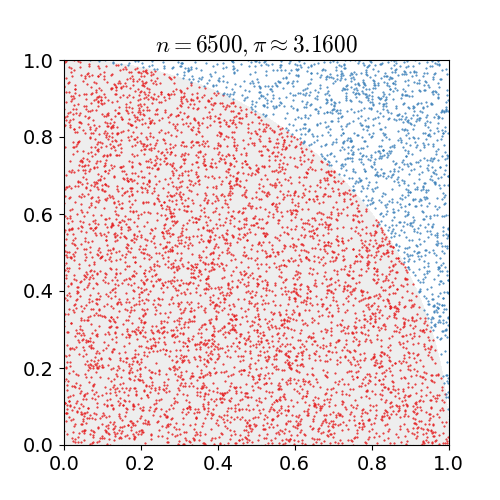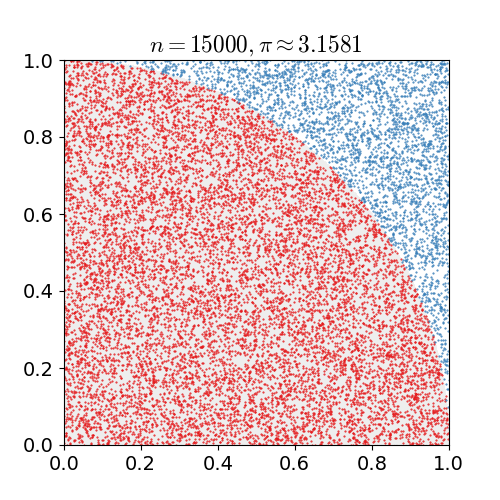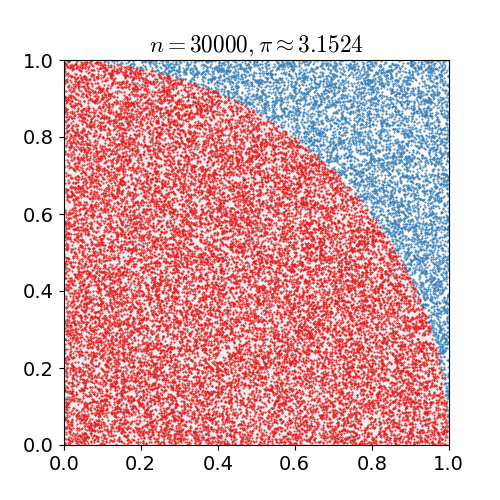
例如经典的求$\pi$方法：首先绘制如图的单位正方形和其中的四分之一圆，然后均匀的在其中随机撒点，统计圆中的点数与总点数比值，该比值即为$\frac{\pi}{4}$

该例中从均匀分布中抽样显然并不困难，也就是可以直接抽样
然而实际问题中的各种概率分布往往都很复杂，不能直接抽样，因此实现蒙特卡罗的关键就是如何从特定概率分布中获得较好的随机抽样

monte_carlo_pi

接受-拒绝采样

假设随机变量$x$的概率密度函数为$p(x)$，接受-拒绝采样寻找一个可以直接采样的分布$q(x)$，满足$cq(x)>p(x)$，其中$c>0$为常数，称$q(x)$为建议分布(proposal distribution)

按照$q(x)$进行采样，假设采样得到$x^$，再按照$\frac{p(x^)}{cq(x^)}$的概率决定是否接受该样本$x^$

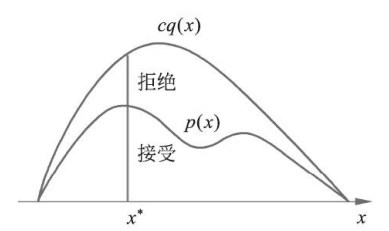
accept-reject

接受-拒绝采样易于实现，但缺点是若$p(x)$体积比$cq(x)$体积小很多，那么接受率就很低，也即效率较低

期望估计和数值积分

蒙特卡罗法在数学中的主要应用就是期望估计和数值积分

期望估计：假设有离散型随机变量$X$，欲求函数$f(x)$的数学期望

$E[f(X)]=\sum_x f(x)P(X=x)$

根据大数定律有

$\lim_{n\to \infty}\sum_{i=1}^n \frac{f(X_i)}{n}=E[f(X)]$

因此可以使用蒙特卡罗进行随机抽样并使用$f(X_i)$的平均值作为期望的近似估计

数值积分：假设有函数$h(x)$，使用蒙特卡罗求其定积分$\int_{\chi} h(x)\mathrm{d}x$的方法称为蒙特卡罗积分

将$h(x)$表示为一个概率密度函数$p(x)$与一个函数$f(x)=\frac{h(x)}{p(x)}$的乘积的形式，则有

$\int_{\chi} h(x)\mathrm{d}x=\int_{\chi} f(x)p(x)\mathrm{d}x=E_{p(x)}[f(x)]$

就可以将任何一个函数的积分表示为数学期望的形式，并使用前述蒙特卡罗方法进行估计

重要性采样

对于期望$E_p[f]=\sum_x f(x)p(x)$，与接受-拒绝采样不同，重要性采样不获得$p(x)$的样本，而是从另一个不同的分布$q(x)$中采样并直接计算期望，即有

$E_{P(X)}[f(X)]=E_{Q(X)}[f(X)\frac{p(X)}{q(X)}]$

记$\hat{E}_Q(f)$为基于分布$Q(x)$获得的期望估计值，则根据蒙特卡罗方法有

$\hat{E}_Q(f)=\frac{1}{N}\sum_{i=1}^Nf(X_i)\frac{p(X_i)}{q(X_i)}$

其中$\frac{p(X_i)}{q(X_i)}$称为重要性权重，这个权重表示我们从$q(x)$中采样到的每个样本在逼近$p(x)$时的重要程度

显然这个期望的估计是无偏估计，但是方差则会受到影响

$Var_{x\sim p}[f(x)]=E_[f(x)^2]-(E_p[f(x)])^2 \\ \begin{aligned} Var_{x\sim q}[f(x)\frac{p(x)}{q(x)}]=&E_q[(f(x)\frac{p(x)}{q(x)})^2]-(E_p[f(x)\frac{p(x)}{q(x)}])^2\\=&E_[f(x)^2\frac{p(x)}{q(x)}]-(E_p[f(x)])^2 \end{aligned}$

重要性采样的方差中多了一个$\frac{p(x)}{q(x)}$，所以如果$p(x),q(x)$两个分布差距过大，就会导致方差很大