聚类的距离度量和性能评估

距离计算

距离是衡量样本间相似度的基本方法，即距离越大相似度越低

有序变量

对于连续型属性或有序的离散型属性，一般使用切比雪夫距离

$$dis(x,y)=\left(\sum_{i=1}^m|x_i-y_i|^p\right)^{\frac{1}{p}}$$

当$p=2$时，切比雪夫距离即欧式距离 $dis(x,y)=|x-y|_2$
当$p=1$时，切比雪夫距离即曼哈顿距离 $dis(x,y)=|x-y|$

二值变量

二值变量指所有属性都是二元离散属性的变量，对二值变量可计算出列联表

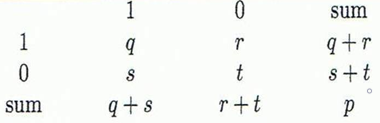
若二值变量为对称变量，即两个状态权重相同，则有

$$dis(x,y)=\frac{r+s}{q+r+s+t}$$

若二值变量为非对称变量，假设正值权重更大，则有Jaccard距离

$$dis_{jaccard}(x,y)=\frac{r+s}{q+r+s}$$

注意Jaccard系数与Jaccard距离的区别，Jaccard系数为 $1-dis_{jaccard}(x,y)=\frac{q}{q+r+s}$

标称型变量

标称型变量指所有属性都是无序离散型属性的变量，也即二值变量的一般推广

其距离可以用简单匹配来衡量，即$dis(x,y)=\frac{p-m}{p}$
其中$p$表示属性个数，$m$表示$x,y$取值相同的属性个数

也可以用VDM(Value Difference Metric)来计算，此处不展开说明

混合变量

一般现实数据集中的样本都包含了各种类型的属性，此时可以使用加权公式来计算样本距离

$$dis(i,j)=\frac{\sum_{f=1}^p\delta_{ij}(f)d_{ij}(f)}{\sum_{f=1}^p\delta_{ij}(f)}$$

当$f$为标称或二值变量时，若$x{if}=x{jf}$，则$d{ij}(f)=0$，否则$d{ij}(f)=1$

性能度量

外部指标

外部指标是指将聚类结果与某个参考模型进行比较

假设当前聚类算法给出的簇划分为$C={C_1,C_2,…,C_k}$，参考模型给出的划分为$C^={C_1^,C_2^,…,C_k^}$，令$\lambda_i,\lambda_i^$分别表示$C_i,C_i^$的均值向量

对所有样本对$(x_i,x_j),i\neq j$，计算出如下列联表

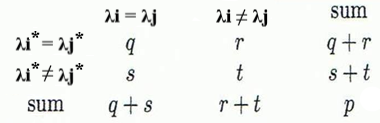
则有如下指标

• Jaccard系数：$J_{Jaccard}=\frac{q}{q+s+r}$
• FM (Fowlkes-Mallows) 指数：$J_{FM}=\sqrt{\frac{q}{q+s}\frac{q}{q+r}}$
• Rand指数：$J_{Rand}=\frac{2(q+t)}{p(p-1)}$

这些指标均为越大越好

内部指标

与外部指标相对的，内部指标直接考察聚类结果

首先作如下定义

• 簇的距离：簇的距离定义为两个簇中最近一对样本的距离，即$d(Ci,C_j)=\min{x\in C_i,y\in C_j}d(x,y)$
• 簇的直径：簇的直径定义为一个簇内最远的一对样本的距离，即$diam(Ci)=\max{x,y\in C_i}d(x,y)$

则有如下指标

• Dunn指数

$$J_{Dunn}=\frac{\min_{i\neq j}d(C_i,C_j)}{\max diam(C_k)}$$

即最近的两个簇间距离与最大簇直径之比，Dunn指数越大越好

• DB (Davies-Bouldin) 指数

记$d_{ij}=|\lambda_i-\lambda_j|$为两个簇均值向量的距离，表示两个簇间的离散程度

$si=\sqrt{\frac{1}{C_i}\sum{x\in C_i}|x-\lambda_i|^2}$为簇内所有样本到均值向量的均方距离，表示簇内的离散程度

$R{ij}=\frac{s_i+s_j}{d{ij}}$表示两个簇间的相似度

则DB指数为

$$J_{DB}=\frac{1}{k}\sum_{i=1}^k \max_{i\neq j}R_{ij}$$

即每个簇与其他簇的最大相似度的平均值，显然DB指数越小越好