聚类(clustering)是一种无监督学习技术

聚类算法试图将数据集中的样本划分为若干个不相交的子集，每个子集称为一个簇(cluster)，每个簇中的样本间包含潜在的联系，也即可能属于同一类

形式化的说，给定样本集$D\in R^{m\times n}$，其中每个样本$x$是一个$m$维向量，聚类算法将$D$划分为$k$个不相交的簇$C1,C_2,…,C_k$，即$C_i\cap{i\neq j}Cj=\emptyset,\ D=\cup{i=1}^kC_i$

显然聚类的目标是使得簇内相似度高，簇间相似度低

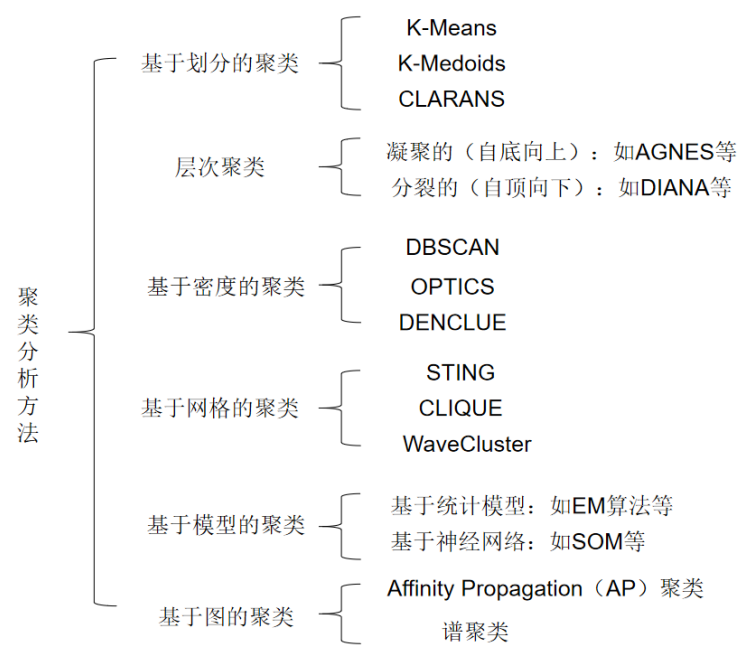
如图所示，聚类的算法很多，下面挑选几个比较基础的进行说明

clustering_summary

K-Means

K-Means属于基于划分的聚类，其基本思想为把相似的点划分为同一类，不相似的点划分到不同类

K-Means算法的目标是最小化如下平方误差

其中 $\mui=\frac{1}{|C_i|}\sum{x\in C_i}x$ 为簇$C_i$的均值向量

该误差表示簇内样本围绕均值向量的紧密程度，$E$越小簇内样本相似度越高

然而最小化该误差是一个NP难问题，因此K-Means采用了贪心策略

K-Means先随机选择$k$个样本作为$k$个簇的初始均值向量$\mu_1,\mu_2,…,\mu_k$
之后每一轮，将各个样本划分到与其距离最近的均值向量所在簇内，再重新计算各个簇的均值向量，直到均值向量不变

如下为K-Means算法的伪码

k-means

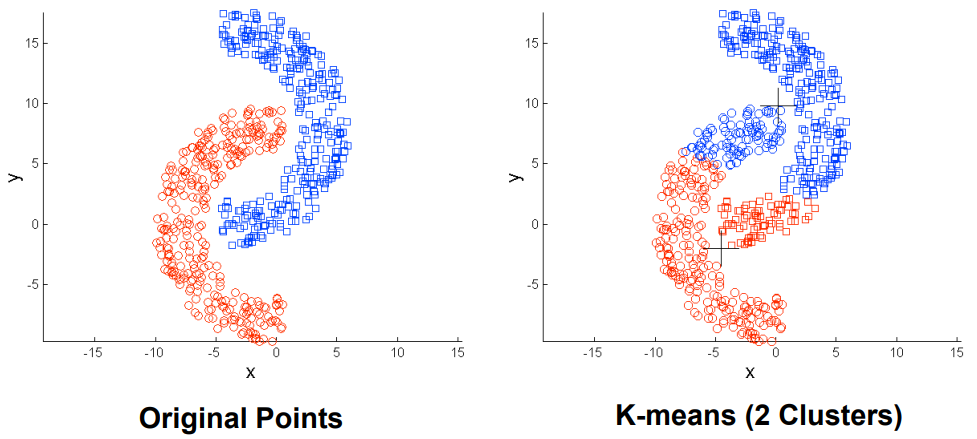
K-Means算法简单高效，是使用最为广泛的聚类算法之一，但是K-Means也有一些明显的缺点
例如易受$k$值和初始簇中心影响，对离群点和噪声敏感，不适合发现大小差别很大的簇等

k-means_nonglobular

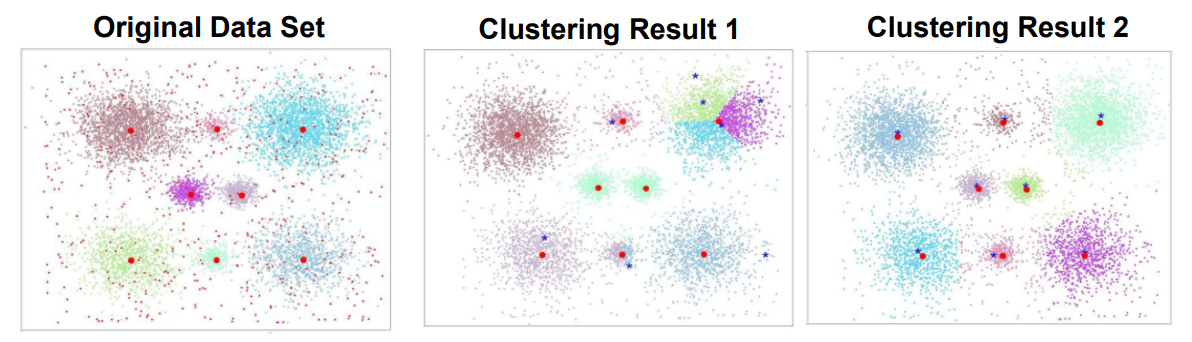
k-means_center

K-Means变种

K-Means算法有很多变种，其目的都是解决K-Means的上述缺陷

二分K-Means

二分K-Means初始时将所有样本划分到一个簇，之后不断选择某个簇执行$k=2$的K-Means，直到簇数达到预设值
其中选择簇的标准是划分后能最大程度减小K-Means的平方误差

该算法主要解决K-Means易受初始簇中心影响的问题

K-Medoids

K-Medoids算法迭代时不使用簇内均值向量，而是使用簇内最靠近中心的样本(medoid)作为参照
medoid满足簇中所有其他样本到该样本距离之和最小

该算法主要解决K-Means易受噪声和孤立点影响的问题

K-median

K-median和K-Means的不同是用L1范数替代L2范数作为距离度量，且用中位值向量替代均值向量

该算法主要解决K-Means易受噪声和孤立点影响的问题

K-Means++

K-Means++的基本思想是，假设当前已选取了$n$个初始簇中心，则距离$n$个已选择初始簇中心越远的样本被选为第$n+1$个初始簇中心的概率越大

也即除第一个初始簇中心外，K-Means++不断根据距离确定加权概率分布来选择剩余$k-1$个初始簇中心

该算法主要解决K-Means易受初始簇中心影响的问题，避免发现较弱聚类

DBSCAN

DBSCAN是一种著名的基于密度的聚类算法，该算法定义了如下概念

  • $\epsilon$邻域：对$x_i\in D$，其$\epsilon$邻域包含$D$中与$x_i$距离不大于$\epsilon$的样本，即

  • 核心对象：若$x_i$的$\epsilon$邻域内至少包含$MinPts$个样本，则$x_i$是一个核心对象

  • 直接密度可达：若$x_j$在$x_i$的$\epsilon$邻域内，且$x_i$是核心对象，则称$x_j$由$x_i$直接密度可达

  • 密度可达：若存在样本序列$p1,p_2,…,p_n$使得$p_1=x_i,p_n=x_j$且$p{i+1}$由$p_i$直接密度可达，则称$x_j$由$x_i$密度可达

  • 密度相连：对$x_i,x_j$，若存在$x_k$使得$x_i$与$x_j$均由$x_k$密度可达，则$x_i$与$x_j$密度相连

给定参数$\epsilon,MinPts$，DBSCAN定义簇$C\subseteq D$为满足如下性质的非空样本子集

  • 对$\forall x_i,x_j\in C$，有$x_i,x_j$密度相连
  • 对$\forall x_i\in C$，若$x_j$由$x_i$密度可达，则$x_j\in C$

根据这个定义，容易发现若$x_i$为核心对象，则由$x_i$密度可达的所有样本构成一个簇

如下为DBSCAN的伪码

DBSCAN

AGNES

AGNES属于层次聚类，其思想是使用树形的聚类结构在不同层次上对数据集进行划分

AGNES是一种自底向上的层次聚类，该算法初始时将每个样本各自看作一个簇，之后不断合并距离最近的两个簇，直到簇数达到预设值

对于簇间距离，有如下度量方法

  • 最小距离：$d{min}(C_i,C_j)=\min{x\in C_i, y\in C_j}d(x,y)$，此时称AGNES为单链接算法
  • 最大距离：$d{max}(C_i,C_j)=\max{x\in C_i, y\in C_j}d(x,y)$，此时称AGNES为全链接算法
  • 平均距离：$d{avg}(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum{x\in Ci}\sum{y\in C_j}d(x,y)$，此时称AGNES为均链接算法
  • 簇中心距离：$d_{center}(C_i,C_j)=d(\mu_i,\mu_j)$，此时称AGNES为中心链接算法