循环神经网络RNN

为了有效利用图像的空间信息，CNN取代了MLP
同样的，对于文本、音频这样含有前后关系的序列化信息，单独处理每个输入的前馈式网络无法有效处理
因此就有了循环神经神网络RNN（Recurrent Neural Net）

文本向量化

分词与词汇表建立

人类的语言多种多样，为了使神经网络更好的理解文本信息，就必须数字化描述文本，这一过程称为文本向量化

文本向量化有三种基本形式

• 将文本按单词分割，并将每个单词转换为一个向量
• 将文本按字符分割，并将每个字符转换为一个向量
• 将文本按n-gram分割，并将每个gram转换为一个向量

将文本分割的过程称为分词（tokenization），而分割出的每个单元称为标记（token）

分词后为了向量化每个token，需要先将其转换为数字形式
即需要建立一个词汇表（Vocabulary），其中包含所有单词到整数的一一映射，然后根据词汇表将单词转换为整数索引

以下面这个包含两个句子的文本为例

str = ['The cat is learning keras', 'but the cat is coding with pytorch']

首先进行单词级分词

[['the', 'cat', 'is', 'learning', 'keras'], ['but', 'the', 'cat', 'is', 'coding', 'with', 'pytorch']]

然后建立词汇表并将文本整数索引化
建立词汇表的方法有很多，例如按单词出现频率顺序给定索引，使用hashing trick等等
不同的索引方法基本只是不同情况下的计算时间效率不同，对神经网络性能没有影响

[[1, 2, 3, 4, 5], [6, 1, 2, 3, 7, 8, 9]]

代码实现

keras中的Tokenizer类可以实现分词与词汇表建立一步到位

from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences

tokenizer = Tokenizer(num_words=10)

text = ['The cat is learning keras', 'but the cat is coding with pytorch']

tokenizer.fit_on_texts(text)  # 获取该文本单词到整数的映射

seq = tokenizer.texts_to_sequences(text)  # 将文本转换为整数索引
# >>> [[1, 2, 3, 4, 5], [6, 1, 2, 3, 7, 8, 9]]

pytorch中稍微复杂一些

import torchtext
from torchtext.vocab import build_vocab_from_iterator
from torchtext.data.functional import numericalize_tokens_from_iterator
from torchtext.data.utils import get_tokenizer

text = ['The cat is learning keras', 'but the cat is coding with pytorch.']

tokenizer = get_tokenizer("basic_english")  # 获取分词器
tokened = [tokenizer(line) for line in text]  # 分词
# >>> [['the', 'cat', 'is', 'learning', 'keras'], ['but', 'the', 'cat', 'is', 'coding', 'with', 'pytorch']]

vocab = build_vocab_from_iterator(tokened)  # 建立词汇表
ids_iter = numericalize_tokens_from_iterator(vocab, tokened)  # 索引生成器
seq = [[num for num in ids] for ids in ids_iter]  # 索引化
# >>> [[4, 2, 3, 8, 7], [5, 4, 2, 3, 6, 10, 9]]

文本索引化后还需要对索引向量化，主要有one-hot编码和词嵌入两种方法

one-hot编码

假设索引的最大值（不同单词的个数）为$n$​​
则每个单词表示为一个n维向量，向量中单词索引位置为1，其余都为0

例如对之前的句子one-hot编码为（句子先0填充至相同长度）

[[[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]  # 0
  [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]  # 0
  [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]  # 1
  [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]  # 2
  [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]  # 3
  [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]  # 4
  [0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]]  # 5

 [[0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]  # 6
  [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]  # 1
  [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]  # 2
  [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]  # 3
  [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]  # 7
  [0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]  # 8
  [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]]]  # 9

代码实现

接上一节keras代码

# ...
from keras.utils import np_utils
import numpy as np

# ...
seq = pad_sequences(seq)  # 句子填充至相同长度
vec = np.array([np_utils.to_categorical(line, num_classes=10) for line in seq])  # 逐句one-hot编码

print(vec)

Tokenizer类的texts_to_matrix方法可以直接转换one-hot，但是和普通one-hot有一些不同
该方法将一个句子表示为一个n维向量，其包含的单词对应的索引位置为1，其余为0

res = tokenizer.texts_to_matrix(text) # 将文本转换为one-hot编码
# >>> [[0. 1. 1. 1. 1. 1. 0. 0. 0. 0.] [0. 1. 1. 1. 0. 0. 1. 1. 1. 1.]]

词嵌入

one-hot编码得到的文本向量有一个缺点
即向量维度可能非常大（可能上万），而且十分稀疏，这些特点会让神经网络学习效率变低
而词嵌入方式将得到低维且密集的向量，其常见的词向量维度只有256或512

获取词嵌入的方式主要有两种

• 让词嵌入作为神经网络的参数与主要任务一起参与学习，即词向量随机初始化，随网络学习而改变
• 使用其他机器学习任务中已计算好的预训练词嵌入

词嵌入要分不同的任务学习而不使用一个通用算法的原因是
文本可能存在不同语言语法结构不同、不同任务中同一语义关系重要性不同等等问题
因此不存在一个对所有文本都完美的词嵌入
这种通过学习向量化文本的方式也是相对one-hot的一个优点

代码实现

keras提供了Embedding层来学习词嵌入
Embedding层能将尺寸为（samples, seq_length）的输入变为（samples, seq_length, embedding_dim）的词嵌入
即将句子中每个单词变成一个embedding_dim维向量

from keras.preprocessing.sequence import pad_sequences
from keras.layers import Embedding

# ['The cat is learning keras', 'but the cat is coding with pytorch.']
seq = [[1, 2, 3, 4, 5], [6, 1, 2, 3, 7, 8, 9]]

seq = pad_sequences(seq)  # 将句子填充为相同长度
# >>> [[0 0 1 2 3 4 5] [6 1 2 3 7 8 9]]

model = Sequential()
model.add(Embedding(10, 2)) 
# 10为不同单词数(索引最大值+1)，2为每个单词向量化的维度
model.compile('adam', 'mse')

vec = model.predict(seq)
print(vec)
'''
>>> [[[-0.00208808 -0.01042473]
  [-0.00208808 -0.01042473]
  [ 0.00661916 -0.00913309]
  [-0.04811562 -0.023326  ]
  [ 0.00657342  0.04661668]
  [ 0.00787752  0.02694471]
  [ 0.00571121  0.00085788]]

 [[ 0.03613539  0.01634348]
  [ 0.00661916 -0.00913309]
  [-0.04811562 -0.023326  ]
  [ 0.00657342  0.04661668]
  [ 0.00215882  0.04187172]
  [-0.04436145 -0.02914215]
  [-0.03849568  0.04484454]]]
'''

循环神经网络RNN

RNN原理

开头说了RNN是为了有效利用序列的前后关系而存在的
而RNN利用的方法就是循环

RNN接受一个尺寸为 (samples, timestep, input_features)的输入
对应到前述的词嵌入即 (samples, 句子单词数, 每个单词向量的维度)

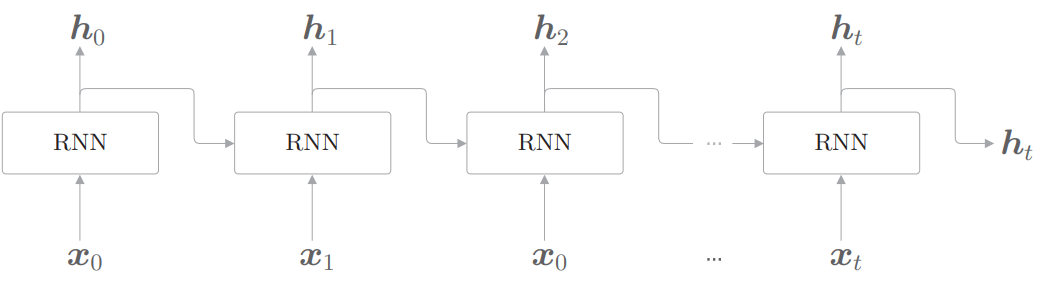
如图所示，其中每个方框称为一个RNN cell
当我们将一个句子送入RNN时，RNN会逐个timestep（逐个单词）地处理句子，即一个cell处理一个单词
第$t$个timestep（第$t$​​​个单词）对应cell的计算为

$$h_t = \mathrm{tanh}(Ux_t+Wh_{t-1})$$

其中$h$​为某个timstep的输出向量，$U$​为对输入$\boldsymbol{x}$​的权重，$W$​​​​​即循环连接的权重
每个cell的$W,U$​​​​是相同的，也即权重共享
RNN就是靠W这条连接做到记忆之前timestep的

显然RNN处理后的输出尺寸为(samples, timesteps, output_features)

注意到因为$ht$​已经包含了对所有$x_1$​到$x{t-1}$​的处理结果
因此RNN也可以只取最后一个输出$h_n$​，即输出尺寸为 (samples, output_features)

keras实现

代码使用了keras内置的“IMDB 电影评论情感分类数据集”
包括25000条电影评论，分为正面/负面评论，文本已按单词出现频率顺序转换为整数索引

keras中的simpleRNN层默认输出尺寸为 (samples, output_features)
若要堆叠多个simpleRNN层，需要传入return_sequences=True，使其输出尺寸为(samples, timesteps, output_features)

SimpleRNN(32, return_sequences=True)

以下为完整代码

import numpy as np
from keras.datasets import imdb
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN, Embedding, LSTM
from keras.utils import np_utils
from keras.preprocessing.sequence import pad_sequences

def getData(mxfeatures, mxlen):
    (X_train, Y_train), (X_test, Y_test) = imdb.load_data(num_words=mxfeatures) # 只要出现频率前10000的单词

    X_train = pad_sequences(X_train, maxlen=mxlen) # 将句子统一长度
    X_test = pad_sequences(X_test, maxlen=mxlen)

    return (X_train, Y_train), (X_test, Y_test)

def buildNet(mxfeatures, input_length):
    model = Sequential()
    model.add(Embedding(mxfeatures, 32, input_length=input_length))

    model.add(SimpleRNN(16))
    model.add(Dense(1, activation='sigmoid'))

    model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

    return model

mxfeatures = 10000
mxlen = 600
(X_train, Y_train), (X_test, Y_test) = getData(mxfeatures, mxlen)

model = buildNet(mxfeatures, mxlen)
model.fit(X_train, Y_train, epochs=3, batch_size=128, validation_split=0.2)

长短期记忆LSTM

LSTM的提出

虽然普通的RNN理论上可以记住所有之前timestep的信息
但实际应用中因为梯度消失，其表现并不那么好

这里的梯度消失和CNN、MLP等前馈式网络的梯度消失有一些不一样
前馈式网络的梯度消失指反向传播时梯度过小无法更新
而RNN的梯度消失是指正向传播中间隔的timestep过长导致信息传递量几乎为0

长短期记忆LSTM（Long Short-Term Memory）的出现就是为了解决这一问题

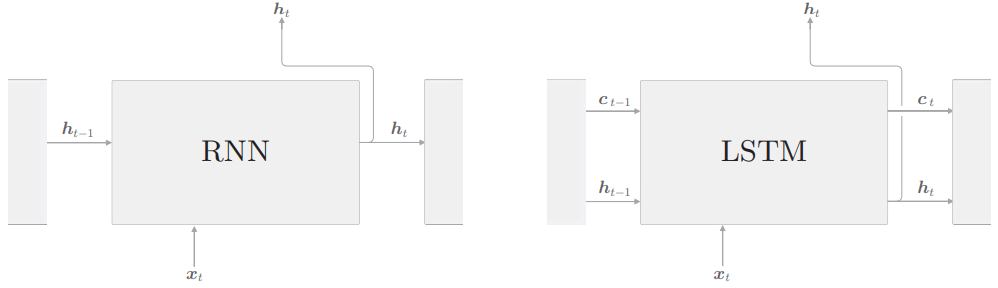
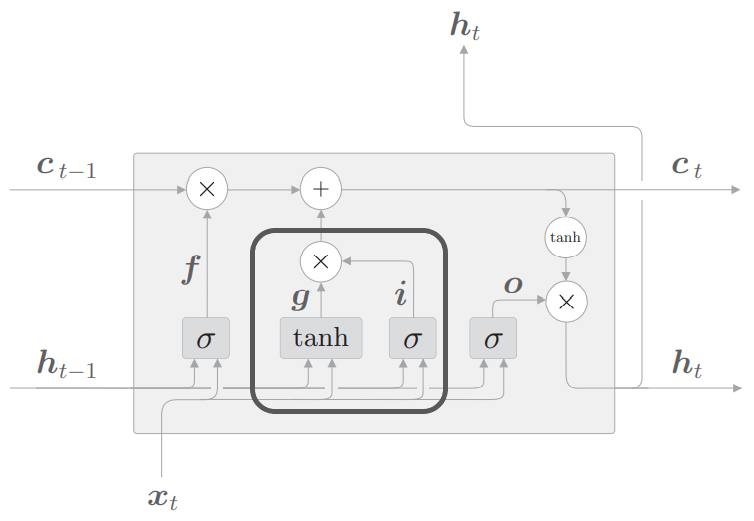
如图所示，LSTM相对RNN多了一条记忆单元$c$
$c$​​的作用是筛选并保存t及t之前timestep的必要信息，而不是像原始RNN一样全部保留

LSTM中的计算基于“门”的思想
可以用水阀类比门，水阀可以控制0~100%的水流量，而门控制数据的传输比率
显然门应该用sigmoid函数激活

LSTM每个cell有三个门，下面依次说明

输出门

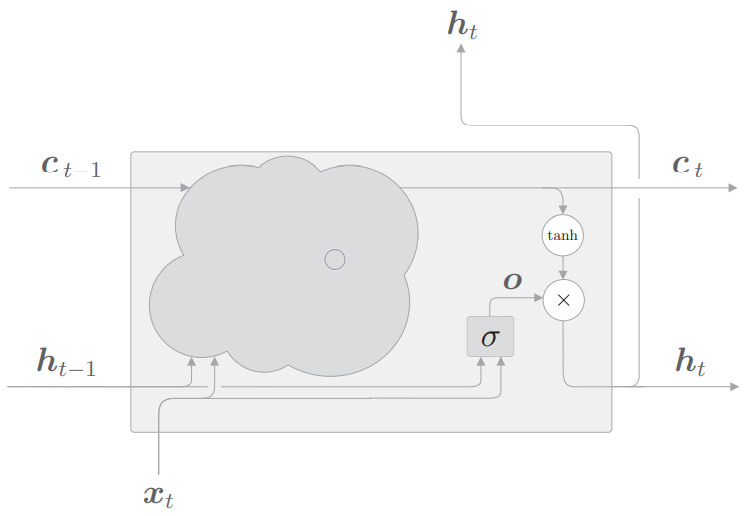
首先输出门的公式为

$$h_t=\sigma(U_ox_t+W_oh_{t-1})\bigodot \mathrm{tanh}(c_t)$$

其中$\sigma(x)$表示sigmoid函数，$\bigodot$表示矩阵对应元素相乘（element-wise multiply）
即$\mathrm{tanh}(ct)$为原输出，$\sigma(U_ox_t+W_oh{t-1})$为对输出的流出比率控制

遗忘门

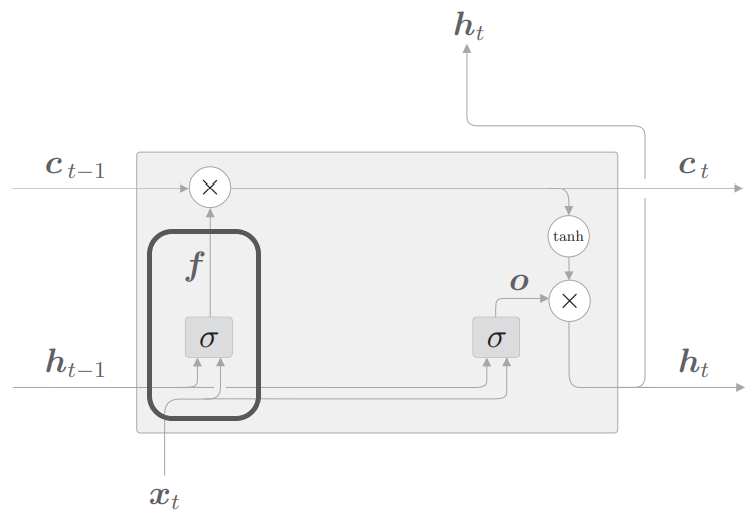
遗忘门公式为

$$f_t=\sigma(U_fx_t+W_fh_{t-1})$$

顾名思义，遗忘门是遗忘之前保留下来的信息$c_t-1$的比例
之后我们将把下式加入到$c_t$的更新中

$$f_t\bigodot c_{t-1}$$

输入门

输入门公式为

$$i_t=\sigma(U_ix_t+W_ih_{t-1}) \\ \tilde{c}_t=\mathrm{tanh}(U_Cx_t+W_Ch_{t-1})$$

之前遗忘门已经完成了对之前timestep的遗忘，现在还需要加入当前timestep的新信息
也即$\tilde{c}_t$表示新信息，$i_t$​表示新信息加入的比例

至此我们就可以得到$c_t$的完整更新公式

$$c_t=f_t\bigodot c_{t-1}+i_t\bigodot \tilde{c}_t$$

注意上述更新公式中不同门的权重矩阵$U, W$​​都是不同的
但是不同LSTM cell的相同门权重矩阵是相同的，也即权重共享

LSTM的输入输出和普通RNN还是一样的
keras中已有LSTM层，只需将上面代码中的simpleRNN换成LSTM即可

门限循环单元GRU

门限循环单元GRU（Gated Recurrent Unit）是一种LSTM的变体
他在大多数情况下表现和LSTM相当，且计算量更小
同样keras中已有GRU层可以直接调用

双向RNN

显然序列有正序和逆序之分，之前的RNN处理都只从一个方向开始顺序处理序列
然而实际中我们并不知道正序和逆序哪个更容易提取信息
这时仅处理一个顺序就可能丢失一些有用信息

应对这种情况就要用到双向RNN
它会用RNN从两个方向分别处理一次序列，并以某种方式合并得到的两个结果

可以用keras中的Bidirectional层实现双向RNN

from keras.layers import SimpleRNN, LSTM, Bidirectional
# ...
# Bidireional默认拼接方式为concat，输出尺寸为(samples, 2*unit)
model.add(Bidirectional(SimpleRNN(16)))
# ...

卷积与RNN

卷积在图像的二维空间信息处理中取得了很大成功
基于同样的思想，我们也可以用一维的卷积处理序列的局部信息

keras中的Conv1D层接受尺寸为(samples, time, feature_dim)的输入
在有padding的情况下输出尺寸相同

同理pooling也可以在序列数据上操作

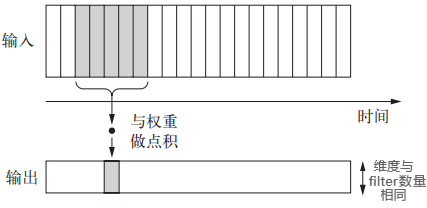
然而，如果只用卷积处理序列，效果可能仍然不会优于RNN
合理的做法是先用多个卷积和池化层提取序列局部特征，再输入RNN处理

以NLP为例，这样做可以先学到一定的上下文关系信息，使得RNN更容易处理
相较于堆叠多个RNN层，这样做的计算代价也会更小