神经网络中常见的激活函数

Sigmoid

$sigmoid(x)=\frac{1}{1+e^{-x}}$

如图左侧是sigmoid图形，右侧是其导数图形

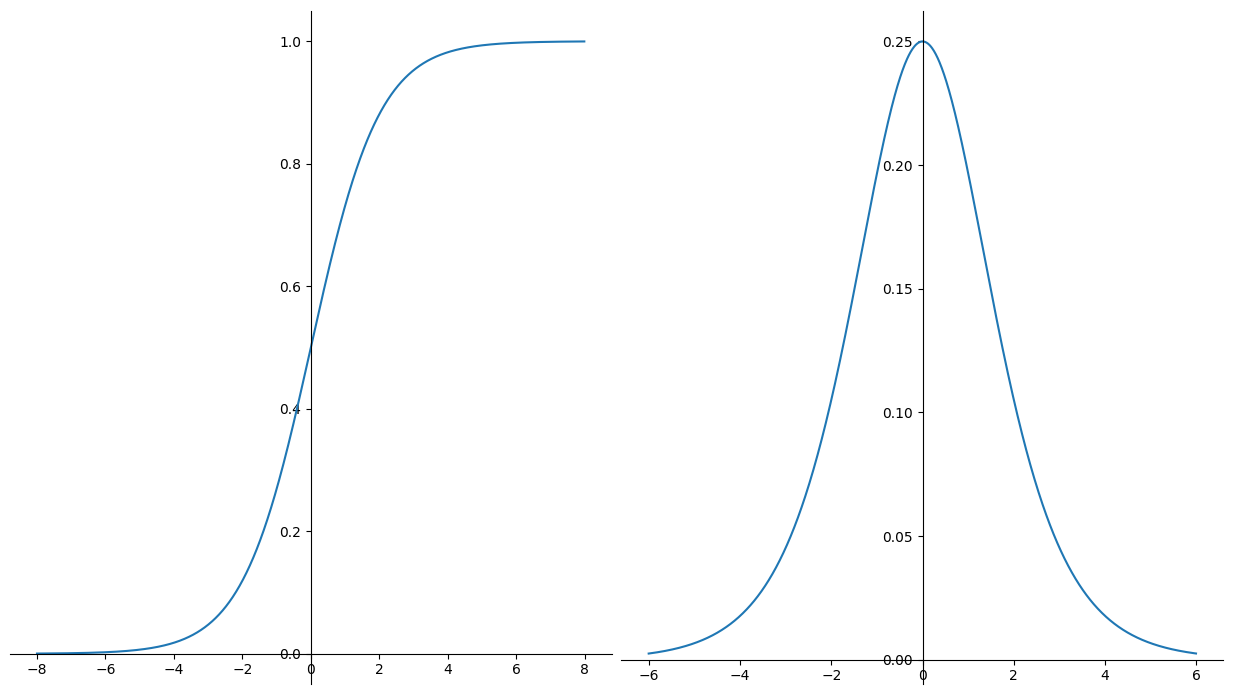
sigmoid

sigmoid是最经典的激活函数
它的主要特点是值域为$[0,1]$，且以0.5为中心，且随着输入增大/减小而无限趋近于1/0

sigmoid有几个比较明显的缺点

我们知道神经网络的反向传播需要以链式法则求梯度
而sigmoid导数最大值为0.25，若反向传播多次经过sigmoid，则梯度会非常接近0，即导致梯度消失

由于sigmoid随增大/减小无限趋近1/0的性质
若激活前的输入x非常大或非常小，则对x的微小更新会使得激活输出值几乎没有变化，进而导致loss也几乎没有变化
此时网络会难以继续学习

即sigmoid输出不是以0为均值的
会导致若神经元输入为正，则反向传播时神经元参数都只能正向更新，反之输入为负则只能都反向更新
这会导致网络收敛较慢

基于上述多种缺点，现在sigmoid已经不在网络中大量使用
只在需要规范化输出在区间[0,1]时使用，例如二分类网络输出层

$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

tanh即双曲正切（Hyperbolic Tangent），下图左侧为tanh图形，右侧为其导数图形

tanh

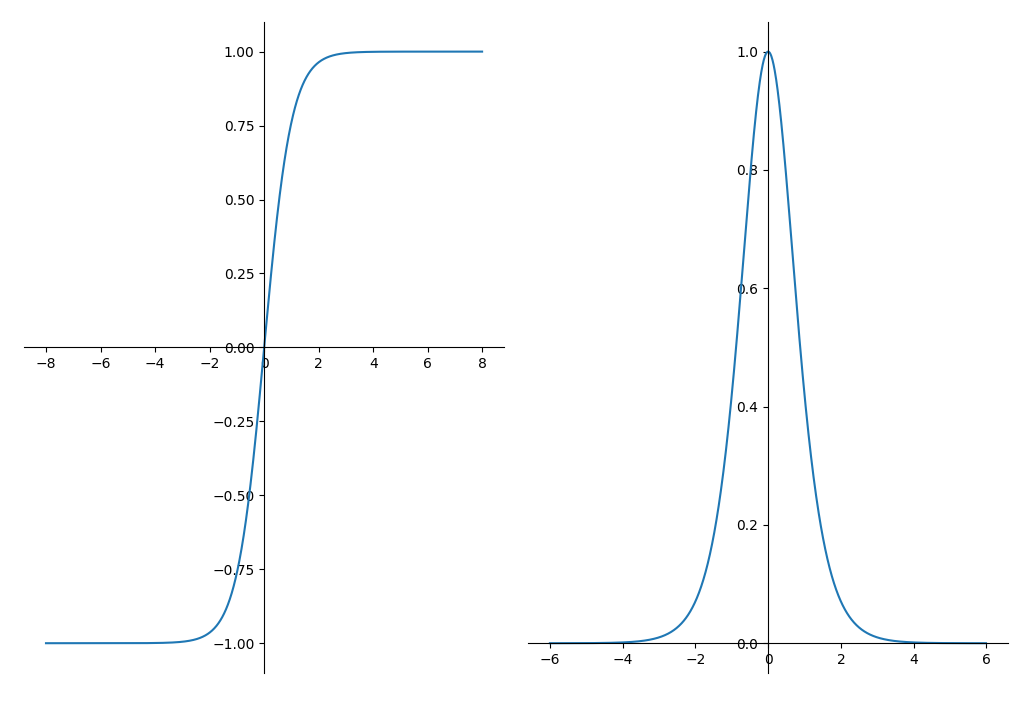
tanh和sigmoid很像，不同之处在于它的值域为$[-1,1]$，而且是zero-centered的
但是梯度消失和饱和以及幂运算的问题并没有解决，因此也只在需要$[-1,1]$的输出时使用

$ReLU(x)=max(0,x)$

ReLU全称为Rectified Linear Unit，即线性修正单元

relu

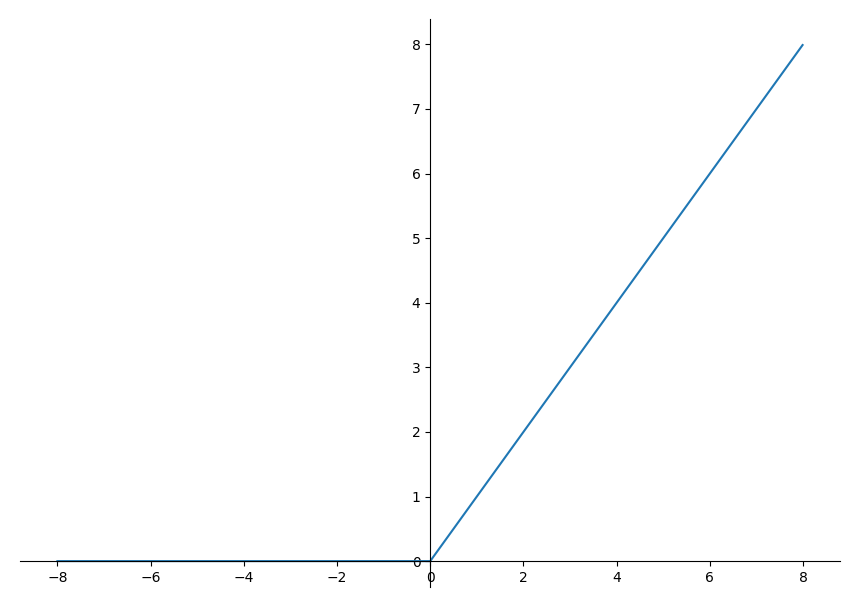
ReLU是现在最常用的激活函数，它的优点有

然而ReLU也有缺点——可能造成神经元死亡
即某些神经元可能永远不会被激活，使得其参数永远无法更新
较好的解决方法是采用合适的初值，例如Xavier初，并保持学习率不要过高

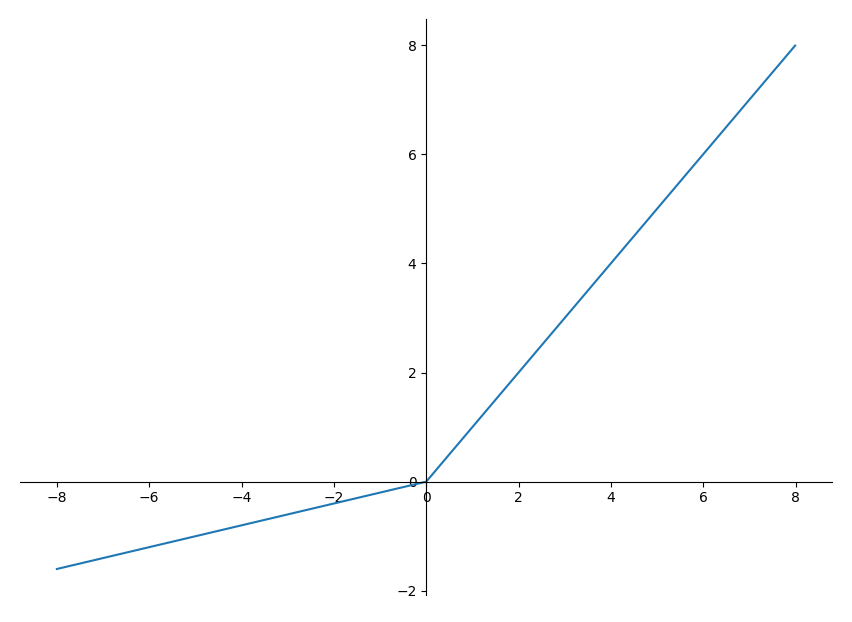
$LeakyReLU(x)=max(\alpha x,x)$

其中$\alpha$为一个很小的常数，使得负数部分斜率不为0
LeakyReLU相较于ReLU解决了神经元死亡问题
注意在实际中，LeakyReLU并没有总是表现出优于ReLU的结果，且相当多的ReLU变种都是如此

leakyrelu

$y_k=\frac{\exp(x_k)}{\sum_{i=1}^n{\exp{x_i}}}$

用于多分类任务规范化输出的激活函数
一般都在网络最后一层和交叉熵损失配合使用，可在此了解交叉熵CrossEntropy详解