什么要CNN

在之前的mnist分类中，我们构造了一个只包含全连接层的网络
为了将图片输入到这样的网络中，我们先对图片进行了一维展开
然而显然图片本身具有二维的空间信息，一维展开相当于直接丢弃了这部分信息
而卷积神经网络CNN（Convolution Neural Net）就是为了更好的利用起这部分信息而存在的

卷积运算

卷积层与滤波

卷积运算与传统图像处理的滤波操作是基本相同的
首先除了图像本身我们需要还一个卷积核
然后对于图像的每一个像素点，计算它的邻域像素和卷积核的对应元素的乘积并累加，作为输出图像该像素位置的值
即完成了一次卷积运算
唯一与滤波不同的是，卷积核的参数是可学习的

conv

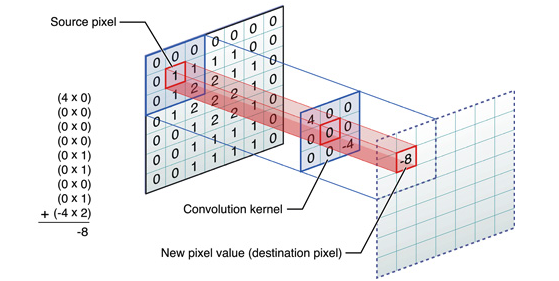
注意到神经网络每层还应该有偏置
在卷积神经层中，偏置也是一个单独的数，会在卷积运算完成后加到输出图像上的每个像素位

一般情况下，我们将卷积层的输入输出数据都成为特征图（feature map）

步幅与填充

卷积运算中每次卷积核移动的步长称为步幅（stride）

显然卷积核步幅越大，卷积完成后的输出特征图尺寸就越小
即使步长为1，输出特征图尺寸相较输入特征图也会缩小

这时候为了保持输出特征图尺寸不变或缩小指定尺寸，就需要填充（padding）
即在输入特征图的四周添加多余的像素点，扩大输入图的尺寸
填充的方法有反射填充、0填充，重复填充等，一般0填充使用较多

假设输入图像尺寸为$(H,W)$，卷积核尺寸为$(FH,FW)$，输出为$(OH,OW)$，填充为$P$，步幅为$S$，则有

三维图像的卷积

很多情况下图像数据并不止二维，它还包含了第三维的颜色通道（channel）
灰度图像是只有1个颜色通道的特例，彩色图像通道方向深度一般是3

这时我们的卷积核也应该是三维的，且第三维深度与图像颜色通道数相同
卷积运算需要对每个通道分别进行，然后将三个通道的输出图对应位置相加（element-wise addition），得到最终的输出特征图

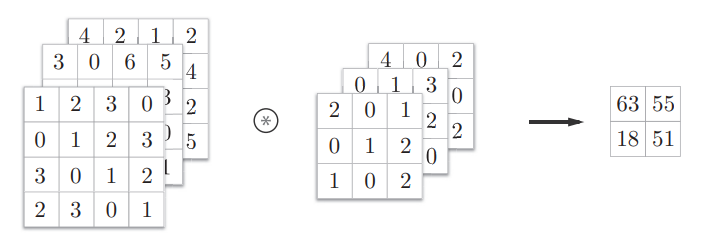
conv_3

我们总是希望CNN中每个卷积层可以多提取信息，但每次卷积后特征图的通道数就变为了1
因此一般每个卷积层都会有不止一个滤波器
设输入数据尺寸为$(C,H,W)$，滤波器尺寸为$(FN,C,FH,FW)$，则输出尺寸为$(FN,OH,OW)$，其中C为通道，FN为滤波器个数

下采样与池化

图像的下采样即降低图像分辨率（缩小尺寸），并尽可能保留关键信息
池化层（Pooling）是卷积神经网络中经典的下采样手段

池化一般分为最大池化和平均池化
以最大池化为例，池化层用一个n×m的窗口依次滑过输入特征图，每次只留下窗口中的最大值

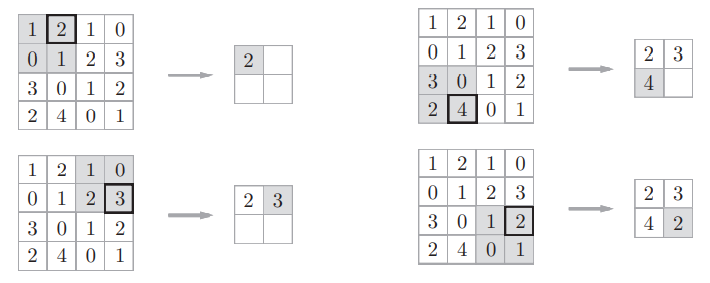
pooling

池化层有一个重要的特征，数据的微小扰动不会对结果造成较大影响

池化层是没有参数的，也即不需要神经网络学习
且池化后特征图的通道数不会发生变化

实际上，池化操作存在很多问题
现在大多数CNN已经不再采用池化，而是直接以带步长的卷积代替了

空洞卷积

空洞卷积（Dilation Convolution）最早出现于图像分割研究中
其目的是代替pooling做减小尺寸并增大感受野的操作

如图所示，空洞卷积就是在卷积域中增加了空洞

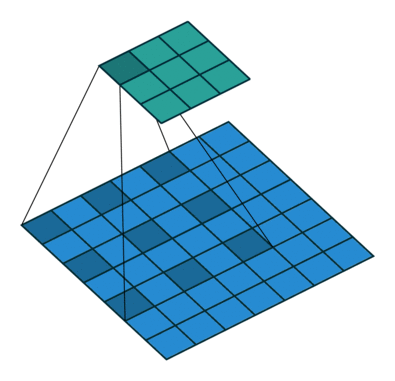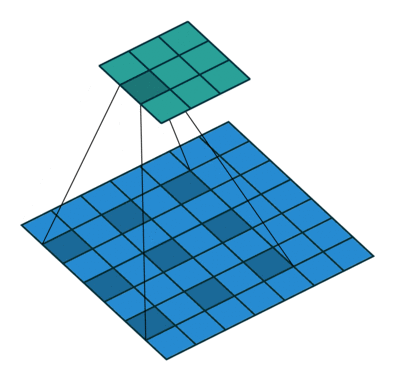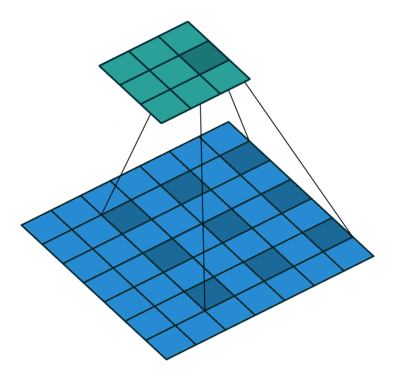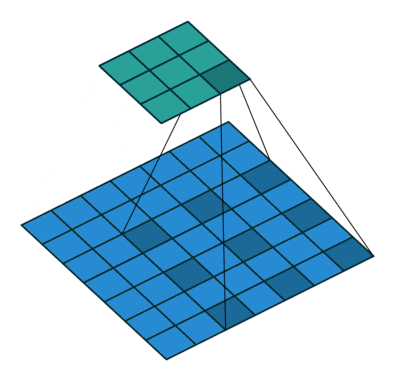
dilation

假设空洞卷积核尺寸为$D$​​​，则卷积层的输入输出尺寸为

​

关于空洞卷积作用的讨论有很多，此处不展开说明

上采样

上采样是和下采样相对的概念，即需要增大图像的分辨率
上采样有三种方法，分别为插值、UpPooling和反卷积

UpPooling即最大池化反向操作，将最大值以外的位置用0填充

反卷积（deconvolution）先按照一定的比例进行0填充扩大尺寸，再进行一次正常卷积

关于UpPooling+Conv实现上采样和反卷积实现上采样的优劣有很多讨论，此处不展开说明

Pytorch使用CNN进行Mnist分类

与Pytorch入门——线性回归与分类中只有网络定义部分不同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Classifier(nn.Module):
    def __init__(self):
        super().__init__()
        
        # pytorch中卷积层张量维度顺序为(batch_size, channel, H, W)
        self.conv1 = nn.Sequential(
            # conv2d参数——输入通道数、输出通道数、卷积核大小、步长、填充大小
            nn.Conv2d(1, 16, kernel_size=5, stride=1, padding=2),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2), # 2x2的最大池化
        )
        self.conv2 = nn.Sequential(
            nn.Conv2d(16, 32, kernel_size=5, stride=1, padding=2),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2),
        )

        self.layer = nn.Linear(7 * 7 * 32, 256)
        self.outputLayer = nn.Linear(256, 10)

    def forward(self, tensor_input):
        x = self.conv1(tensor_input)
        x = self.conv2(x)

        x = x.view(x.size(0), -1)  # 一维展开,展开为后(batch_size, channel*H*W)
        x = self.layer(x)
        out = self.outputLayer(x)

        return out

Keras使用CNN进行Mnist分类

与Keras入门——线性回归与分类中只有网络定义部分不同

注意keras以tensorflow为后端时默认的图片通道在第三维

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def buildNet():
    model = Sequential()

    # output_shape(28, 28, 32)
    model.add(Conv2D(
        input_shape=(28, 28, 1),
        filters=32,  # 滤波器个数
        kernel_size=(5, 5),  # 卷积核大小
        # strides=(1, 1), 卷积沿宽度和高度方向的步长,默认(1,1)
        padding='same',  # 边缘填充方法,可选"valid"/"same","valid"-不填充,"same" 填充以使图片维度不变
        data_format='channels_last', # 指定通道在哪一维度
        # dilation_rate=(1,1), 膨胀卷积的膨胀率
        # use_bias=True, 该层是否使用偏置向量
        # activation, 激活函数
    ))
    model.add(Activation('relu'))

    # output_shape(14, 14, 32)
    model.add(MaxPooling2D(
        pool_size=(2, 2), # # 2x2窗口的最大池化
        strides=(2, 2), # 步长,如果是None则使用pool_size
        padding='same',
    ))

    model.add(Conv2D(filters=64, kernel_size=(5, 5), padding='same', activation='relu'))  # output_shape(14, 14, 64)
    model.add(MaxPooling2D(pool_size=(2, 2), padding='same'))  # output_shape(7, 7, 64)

    model.add(Flatten())  # 一维展开，无学习参数

    model.add(Dense(256, activation='relu'))
    model.add(Dropout(0.25)) # 引入dropout防止过拟合,rate表示丢弃的比例

    model.add(Dense(10, activation='softmax'))

    model.compile(optimizer=Adam(lr=1e-4), loss='categorical_crossentropy', metrics=['accuracy'])

    print(model.summary())
    return model