感知机

什么是感知机

感知机是神经网络的起源算法
在理解感知机的基础上我们可以了解到现代神经网络是如何一步步演化来的

如图所示就是一个感知机，其中$x_1,x_2$为输入信号，$y$为输出信号，$w_1,w_2$为连接权，$b$称为偏置
这个感知机表示函数

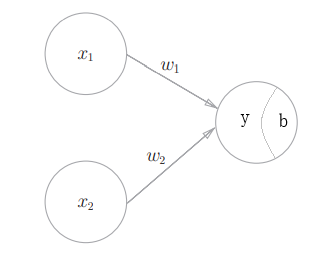
perceptron

显然通过合理设定$w_1,w_2$，这样一个感知机模型可以表示出与门、或门、与非门等
例如$(w_1,w_2,b)=(0.5,0.5,0.7)$时这个感知机就构成了一个与门
又显然可以有多组不同的$(w_1,w_2,b)$使得感知机构成与门

同理对或门、与非门等也是如此，这体现出感知机具有一定的表示非线性关系的能力

多层感知机

现在已知感知机有表示非线性关系的能力，考虑使用上述感知机来构造异或门
但这时我们发现无论如何构造权值都无法满足要求

试着形象化这个问题，即要用一条直线将圆点和三角点分隔开，这显然不可能

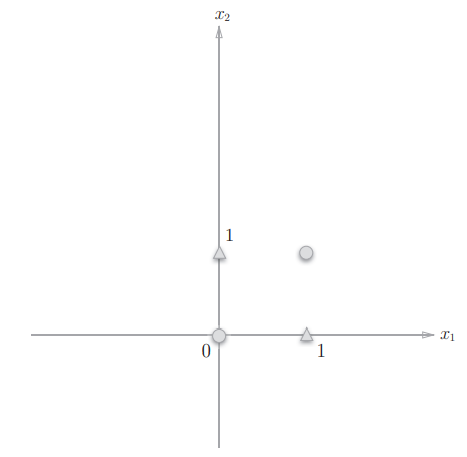
perceptron_xor

然而我们已知异或门可以由与门、或门、与非门等的组合表示
这启发我们类似组合基本门一样堆叠感知机

如图所示（图中偏置未标出），$x_1,x_2,s_1$组成的感知机构成与非门，$x_1,x_2,s_2$组成的感知机构成或门，$s_1,s_2,y$组成的感知机构成与门
这样我们就通过堆叠感知机获得了一个异或门

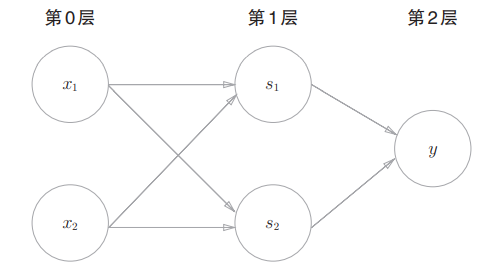
perceptron_multi

我们将堆叠起来的感知机称为多层感知机
异或门的例子说们多层感知机可以有更强的非线性表示能力

从感知机到神经网络

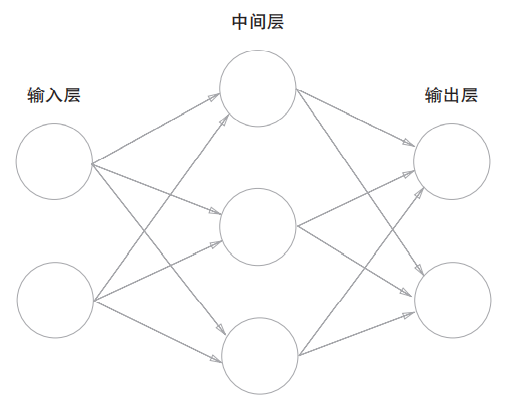
上述的多层感知机其实已经非常接近神经网络模型了

如下图所示，神经网络包含一个n维输入层，一个m维输出层，中间层也称为隐藏层
层于层之间都是全连接，且运算方式和多层感知机基本一致

这样的神经网络称为前馈式神经网络，其完成一次从输入到输出的计算称为一次前向传播
为了具有比多层感知机更强的非线性表示能力，神经网络在多层感知机基础上引入了激活函数

nn

激活函数

回忆感知机的函数表示

我们将其改写为$y=h(w_1x_1+w_2x_2-b)$

其中$h(x)$就是激活函数，在感知机中激活函数为

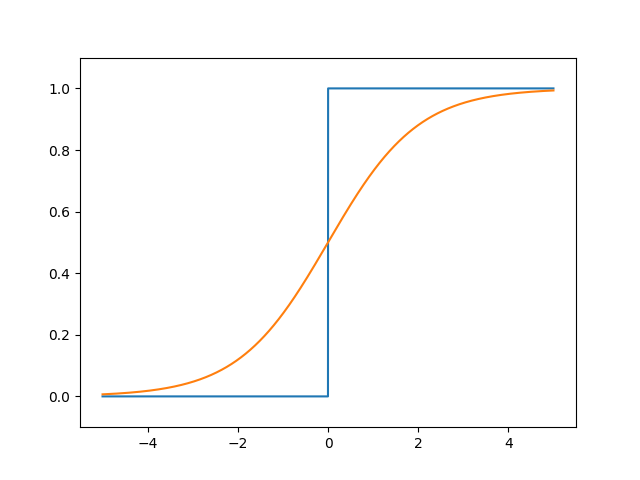
这样的函数称为阶跃函数（图中蓝线）
由于其导数恒为0，且不连续，会导致表示能力弱、神经网络参数难以更新等问题

对比神经网络常用的sigmoid函数（图中橘线）

可以明显看出两者值域都在0~1间，但sigmoid具有平滑、连续的特点

这样的激活函数相对于阶跃函数对神经网络的学习有很多优点

activation

其他常用的激活函数还有Softmax、ReLU、Tanh等等
可以看这里 神经网络中常见的激活函数 了解

神经网络的学习

损失函数

上述感知机模型中我们已知目标函数，因此可以直接为其赋值
但通常情况下我们并不知道神经网络所要学习的目标函数
因此神经网络所表示的函数与目标函数的误差就只能通过网络输出值与真实值的误差体现出来
而衡量这个误差就需要引入损失函数

记网络输出值（第k维）为$\hat{y_k}$，真实值为$y_k$，常见的损失函数如下

  • 绝对误差MAE：$E=\sum_k|\hat{y_k}-y_k|$
  • 均方误差MSE：$E=\sum_k(\hat{y_k}-y_k)^2$
  • 交叉熵误差CrossEntropy：$E=-\sum_ky_k\log{\hat{y_k}}$

其中交叉熵误差用于分类学习，详细解释可以看这里 交叉熵CrossEntropy详解

再谈损失函数的引入

回顾引入损失函数的原因，为什么衡量误差不能直接用准确率呢
理由和激活函数选择抛弃阶跃函数相似

若以准确率作为衡量标准，参数的导数在大多数地方会变成0，使得参数难以更新

例如网络在100张猫的图片中识别出37张猫的图片，则准确率为37%
此时仅仅微调参数，准确率可能不会变化，也就不能为下一次参数更新提供参考

其次准确率的值不连续也使得的学习很难进行

Mini-batch学习

通常训练神经网络所用的数据集十分大，可能为百万甚至千万级
受限于硬件条件，我们往往不可能一次性将所有数据送入网络，因此需要mini-batch学习
即每次从数据集中随机选取一个batch的数据送入网络学习

一个batch的大小可以是任意值，通常会取16、32，64、128等二的次幂

mini-batch学习中网络需要衡量一个batch数据的整体误差，也即需要对一个batch的损失求平均值
例如均方误差为$E=\frac{1}{N}\sum\sum_k(\hat{y_k}-y_k)^2$

梯度下降法

上述感知机模型中权值我们都是手动设定的
但神经网络的参数量显然不能再依靠手动设置，此时就要引入梯度下降法

我们假设目标函数为$f(x_1,x_2,…,x_n)$，并假设它是一个凹函数
其任意一点梯度为${\frac{\partial{f}}{\partial{x_1}},\frac{\partial{f}}{\partial{x_2}},…,\frac{\partial{f}}{\partial{x_n}}}$

我们给$\boldsymbol{x}$​指定任意初始值，梯度下降法每次令$x_i\leftarrow x_i-\eta\frac{\partial{f}}{\partial{x_i}}$​
其中常数$\eta$称为学习率，通常指定为一个较小值，如0.01或0.001

梯度下降法的含义就是不断小步地沿着梯度方向朝目标函数极小值点靠近

学习率过大可能导致梯度下降法不断在极值点附近震荡而不能到达极值点
而学习率过小可能导致神经网络训练效率底

误差反向传播法

为了将梯度下降法应用于神经网络的参数
我们需要求损失函数对各层参数的梯度

误差反向传播(BP)算法就是求解这些梯度的算法
反向传播的含义在于求梯度过程需要利用求导的链式法则从网络最后一层开始依次反向计算每一层的梯度

求梯度的具体实现中使用了称为计算图的方法，此处不再展开说明

梯度下降法的深入

利用BP算法完成神经网络每层参数当前梯度的计算后
若直接按照公式$x_i=x_i-\eta\frac{\partial{f}}{\partial{x_i}}$更新参数，则称为随机梯度下降法SGD

SGD虽然实现简单，但在一些问题的求解上可能效率并不高
因此许多其他参数更新器陆续被提出，例如Momentum、Adam、AdaGrad等等
我们将这些参数更新器称为optimizer或solver
可以看这里详细了解 神经网络中常见的optimizer

总结

文中已经解释了神经网络大部分基础理论
接下来可以试着直接上手pytorch、tensorflow或keras边码边学习深入的内容