SGD

梯度下降法（gradient descent）是最经典的神经网络参数更新方法，其表达式为

其中$\boldsymbol{W}$为参数矩阵，$\frac{\partial L}{\partial \boldsymbol{W}}$为梯度，$\eta$为学习率

梯度下降法有BGD、SGD、MBGD三种
批量梯度下降BGD是每次参数更新都用所有样本计算梯度
随机梯度下降SGD是每次随机选择一个样本计算梯度
而小批梯度下降MBGD则是前两者的折中，每次计算一个mini-batch样本的梯度

BGD由于每次更新都要用到所有样本，所以收敛较慢
而SGD由于每次更新使用样本少，可能导致陷入局部最优
所以实际中一般都采用MBGD

需要注意的是，大部分神经网络框架中的SGD指的就是MBGD

抛开样本量的问题只关注梯度下降法的数学形式
会发现朴素的梯度下降在一些情况下有效率较低的缺点
考虑目标函数$f(x,y)=\frac{1}{10}x^2+y^2$，如图所示

sgd

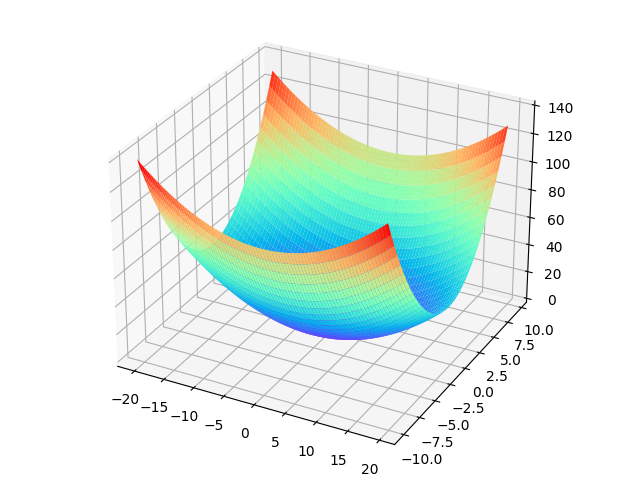
这个函数图形是碗状的，但是不对称
可以明显发现该函数沿x轴方向梯度变化不大，而y轴方向梯度相对较大
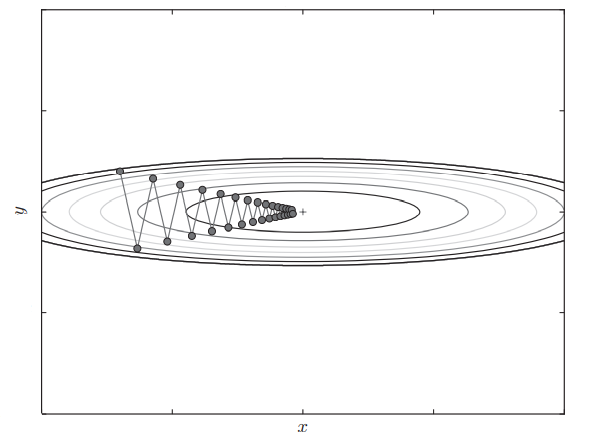
此时SGD就会“之字形”移动

也即，如果函数的形状是非均向的，SGD的效率就会较低

sgd2

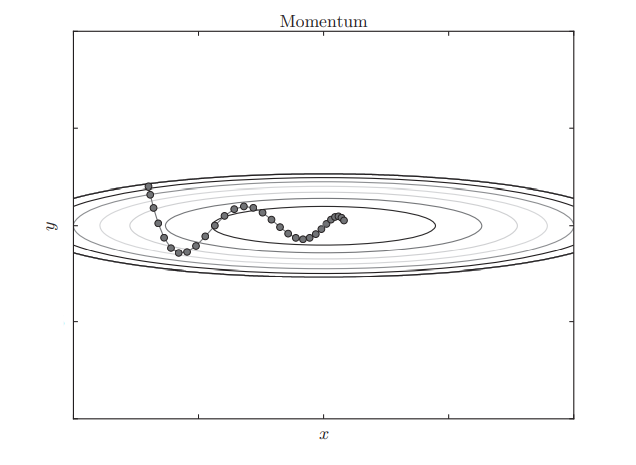
Momentum

Momentum意为动量，其表达式为

其中$\boldsymbol{v}$用于记忆历史的梯度，$\alpha$一般设为0.9左右
假如当前梯度和历史梯度方向相同，那么$\boldsymbol{v}$就越来越大，更新就会变快
反之当前梯度方向和历史梯度不同，更新量就会减少

Momentum的更新方法可以用小球类比
让小球从碗边释放，小球开始会高速滚下，接近碗底后会来回摆动且速度不断减小并最终稳定

仍以$f(x,y)=\frac{1}{10}x^2+y^2$为例，Momentum更新过程将会如下图所示

momentum

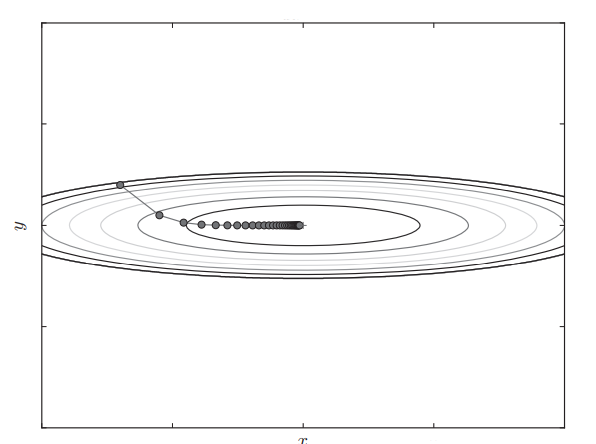
AdaGrad

AdaGrad即Adaptive Gradient
它的思想是学习率衰减，即随着学习进行，学习率逐渐减小

其中$\bigodot$表示矩阵对应元素相乘，即AdaGrad保存了历史梯度平方和

还是之前的函数，AdaGrad学习过程如图

adagrad

RMSProp

AdaGrad有一个缺点，即随着学习不断进行，学习率越来越小，最终参数更新量会无限趋近0
RMSProp最是为了改进这一个缺陷而被提出的

其中$\rho$为衰减因子，一般设为0.9左右
相较AdaGrad记住所有历史梯度，RMSProp会对历史梯度逐渐遗忘
易知因为衰减因子的存在，对历史梯度的记忆会随着学习进行呈指数式减小

Adam

adam是一个比较新的optimizer，同时借鉴了动量和学习率衰减思想，现在也比较常用